题目内容
4.先化简,后求值:(1)$\frac{3}{2}$m-($\frac{5}{2}$m-1)+3(4-m),其中m=-3.
(2)5a2b-[2a2b-2(ab2-2a2b)]-2ab2,其中a=-$\frac{1}{2}$,b=4.
(3)如果代数式(2x2+ax-y+1)-(2bx2-3x+5y-4)的值与字母x所取的值无关,试求代数式$\frac{1}{3}{a^3}-2{b^2}-({\frac{1}{4}{a^3}-3{b^2}})$的值.
分析 (1)(2)先去括号合并化简,再进一步代入数值求得答案即可;
(3)先去括号合并化简,利用含x的项为0,求得a、b,进一步化简代数式,代入数值求得答案即可.
解答 解:(1)原式=$\frac{3}{2}$m-$\frac{5}{2}$m+1+12-3m
=-4m+13
当m=-3时,
原式=25;
(2)原式=5a2b-[2a2b-2ab2+4a2b]-2ab2
=5a2b-6a2b+2ab2-2ab2
=-a2b
当a=-$\frac{1}{2}$,b=4时,
原式=-1;
(3)(2x2+ax-y+1)-(2bx2-3x+5y-4)
=2x2+ax-y+1-2bx2+3x-5y+4
=(2-2b)x2+(a+3)x-6y+5
∵代数式的值与字母x所取的值无关,
∴2-2b=0,a+3=0
∴a=-3 b=1;
则-$\frac{1}{3}{a^3}-2{b^2}-({\frac{1}{4}{a^3}-3{b^2}})$
=-$\frac{7}{12}$a3+b2
=$\frac{67}{4}$.
点评 此题考查整式的化简求值,掌握去括号的方法与合并同类项的方法是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
15. a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
 a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )
a、b在数轴上的位置如图所示,那么化简$|{a-b}|-\sqrt{a^2}$的结果是( )| A. | 2a-b | B. | b | C. | -b | D. | -2a+b |
9. 如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
 如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )
如图,数轴上两点所表示的数分别为m、n,则下列各式中成立的是( )| A. | m+n>0 | B. | m+n<0 | C. | m-n>0 | D. | m-n=0 |
14.为了迎接期中考试,小强对考试前剩余时间作了一个安排,他把计划复习重要内容的时间用一个四边形圈起来.如图,他发现,用这样的四边形圈起来五个数的和恰好是5的倍数,他又试了几个位置,都符合这样的特征.
(1)若设这五个数中间的数为a,请你用整式的加减说明其中的道理.
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
(2)这五个数的和能为150吗?若能,请写出中间那个数,若不能,请说明理由.
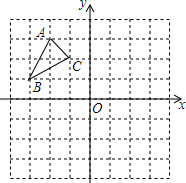 如图,△ABC中A(-2,3),B(-31),C(-1,2).
如图,△ABC中A(-2,3),B(-31),C(-1,2).