题目内容
1.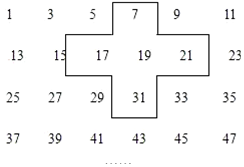 实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)
实践与探索:将连续的奇数1,3,5,7…排列成如图的数表用十字框框出5个数(如图)(1)若将十字框上下左右平移,但一定要框住数列中的5个数,若设中间的数为a,用a的代数式表示十字框框住的5个数字之和;
(2)十字框框住的5个数之和能等于2015吗?若能,分别写出十字框框住的5个数;若不能,请说明理由;
(3)十字框框住的5个数之和能等于365吗?若能,分别写出十字框框住的5个数;若不能,请说明理由.
分析 (1)观察十字框框住的数据的排列规律得到其他四个数为a-12,a-2,a+2,a+12,然后利用合并同类项求5个数的和;
(2)解方程5a=2015得a=403,由于十字框框内的数都是奇数,所以十字框框住的5个数之和能等于2015;
(3)解方程5a=365,解得a=73,然后确定73所在位置即可.
解答 解:(1)从表格知道中间的数为a,上面的为a-12,下面的为a+12,左面的为a-2,右面的为a+2,
a+(a-2)+(a+2)+(a-12)+(a+12)=5a;
(2)5a=2015,
a=403,
∵403是奇数,
∴这个是可以的;
(3)5a=365,
a=73,
∵73位于一行的最左边,
∴十字框框住的5个数之和不能等于365.
点评 本题考查了一元一次方程的应用,首先审题找出题中的未知量和所有的已知量,直接设要求的未知量或间接设一关键的未知量为x,然后用含x的式子表示相关的量,找出之间的相等关系列方程、求解、作答,即设、列、解、答.

练习册系列答案
相关题目
6. 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
 如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )
如图,△ABC中,∠C=90°,AC=BC,AD是∠BAC的角平分线,DE⊥AB于E,若AB=10cm,则△DBE的周长等于( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 9cm |
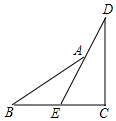 如图,阅读下面的题目及分析过程,并按要求进行证明.
如图,阅读下面的题目及分析过程,并按要求进行证明.