题目内容
14.计算:(1)5$\sqrt{\frac{1}{5}}$-$\sqrt{20}+2\sqrt{45}$
(2)($\sqrt{12}+5\sqrt{8}$)×$\sqrt{3}$
(3)$\sqrt{18}÷$(-$\sqrt{\frac{3}{4}}$)×$\sqrt{\frac{4}{3}}$
(4)(2$\sqrt{5}+\sqrt{3}$)($\sqrt{3}-2\sqrt{5}$)
分析 (1)首先对二次根式进行化简,然后合并同类二次根式即可;
(2)首先利用分配律计算,然后进行化简即可;
(3)首先转化为乘法计算,然后化简即可;
(4)利用平方差公式即可求解.
解答 解:(1)原式=$\sqrt{5}$-2$\sqrt{5}$+6$\sqrt{5}$=5$\sqrt{5}$;
(2)原式=$\sqrt{12}$×$\sqrt{3}$+5$\sqrt{8}$×$\sqrt{3}$=6+10$\sqrt{6}$;
(3)原式=-$\sqrt{18×\frac{4}{3}×\frac{4}{3}}$=-4$\sqrt{2}$;
(4)原式=($\sqrt{3}$)2-(2$\sqrt{5}$)2=3-20=-17.
点评 本题考查了二次根式的化简求值,正确理解二次根式的运算性质,正确进行化简是关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
19.计算$\sqrt{\frac{1}{2}ab}•\sqrt{\frac{1}{6}a}$的最终结果是( )
| A. | $\frac{1}{12}|a|b$ | B. | |a|$\sqrt{\frac{b}{12}}$ | C. | $\frac{a\sqrt{3b}}{6}$ | D. | -$\frac{a\sqrt{3b}}{6}$ |
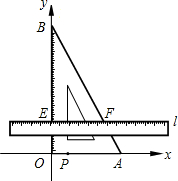 如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.
如图,把含有30°角的三角板ABO置入平面直角坐标系中,A,B两点坐标分别为(3,0)和(0,3$\sqrt{3}$).动点P从A点开始沿折线AO-OB-BA运动,点P在AO,OB,BA上运动,速度分别为1,$\sqrt{3}$,2(长度单位/秒)﹒一直尺的上边缘l从x轴的位置开始以$\frac{\sqrt{3}}{3}$(长度单位/秒)的速度向上平行移动(即移动过程中保持l∥x轴),且分别与OB,AB交于E,F两点﹒设动点P与动直线l同时出发,运动时间为t秒,当点P沿折线AO-OB-BA运动一周时,直线l和动点P同时停止运动.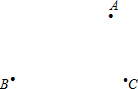 如图,已知点A,B,C,根据下列要求画图.
如图,已知点A,B,C,根据下列要求画图.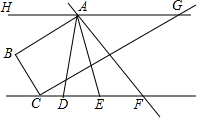 如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG. 如图,有一条直的宽纸带,按图折叠,则∠α的度数等于75°.
如图,有一条直的宽纸带,按图折叠,则∠α的度数等于75°.