题目内容
14.某商店经销一种销售成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500kg,销售单价每涨1元,月销售量就减少10kg,设销售单价为每千克x元,月销售利润为y元.(1)当销售单价定为每千克55元时,计算销售量和月销售利润;
(2)求y与x之间的函数关系式,并说明当销售单价应定为多少时,月销售利润最大?最大利润是多少?
(3)商店想在销售成本不超过10000元的情况下,使得月销售利润刚好达到8000元,销售单价应为多少?
分析 (1)根据题意计算即可;
(2)利润=销售量×单位利润.单位利润为x-40,销售量为500-10(x-50),据此表示利润得关系式,进而得出最大利润;
(3)销售成本不超过10000元,即进货不超过10000÷40=250kg.根据利润表达式求出当利润是8000时的售价,从而计算销售量,与进货量比较得结论.
解答 解:(1)销售量:500-5×10=450(kg);
销售利润:450×(55-40)=450×15=6750(元);
(2)由题意可得:
y=(x-40)[500-10(x-50)]
=-10x2+1400x-40000
=-10(x-70)2+9000,
故当销售单价应定为70时,月销售利润最大,最大利润是9000元;
(3)由于水产品不超过10000÷40=250kg,定价为x元,
则(x-40)[500-10(x-50)]=8000
解得:x1=80,x2=60
当x1=80时,进货500-10(80-50)=200kg<250kg,符合题意,
当x2=60时,进货500-10(60-50)=400kg>250kg,舍去.
答:销售单价应为80元.
点评 本题考查了一元二次方程的应用及根据实际问题列二次函数关系式.关键是设售价,分别表示每件利润和销售量,根据求利润的公式列出关系式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.当a>0时,下列关于幂的运算正确的是( )
| A. | a0=0 | B. | a-1=-a | C. | (-a)2=-a2 | D. | a-2=$\frac{1}{{a}^{2}}$ |
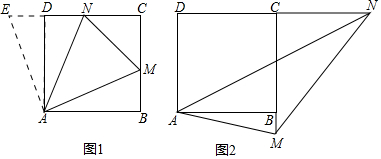
9. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
6.使分式$\frac{1}{x+2}$有意义的条件是( )
| A. | x≠-2 | B. | x≠2 | C. | x≠±2 | D. | x>-2 |
3.一次函数y=x+2的图象与x轴交点的坐标是( )
| A. | (0,2) | B. | (0,-2) | C. | (2,0) | D. | (-2,0) |
4.观察下表规律,
利用规律如果$\root{3}{2.37}$=1.333,$\root{3}{23.7}$=2.872,则$\root{3}{0.0237}$=0.2872.
| a | 0.008 | 8 | 8000 | 8000000 |
| $\root{3}{a}$ | 0.2 | 2 | 20 | 200 |
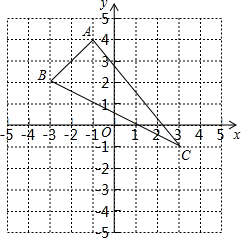 如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).
如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).