题目内容
7.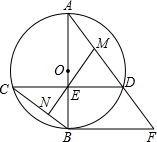 如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.
如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.
分析 连接BD,由于∠A、∠C所对的弧相同,因此cosA=cosC,在Rt△ABF中,cos∠A=$\frac{AB}{AF}$=$\frac{4}{5}$,设AB=4x,则AF=5x,由勾股定理得:BF=3x.因为BF=6,解出x=2,从而得到直径AB的长,也就能求出⊙O的半径.
解答 解:连接BD.
∵∠BCD与∠BAF同对$\widehat{BD}$,
∴∠C=∠A,
∴cos∠A=cos∠C=$\frac{4}{5}$,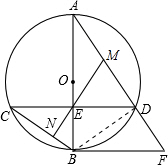
∵BF是⊙O的切线,
∴∠ABF=90°
在Rt△ABF中,cos∠A=$\frac{AB}{AF}$=$\frac{4}{5}$,
设AB=4x,则AF=5x,由勾股定理得:BF=3x.
∵BF=6,∴x=2,
∴直径AB=4x=4×2=8,
则⊙O的半径为4.
点评 本题考查了切线的性质,圆周角定理,锐角三角函数,解直角三角形,辅助线的作法是解题的关键.

练习册系列答案
相关题目
19.方程$\frac{1}{1+x}$=$\frac{2}{1-{x}^{2}}$+1的解为( )
| A. | 0 | B. | -1 | C. | 2 | D. | -1或2 |
16.矩形具有而菱形不具有的性质是( )
| A. | 对角线相等 | B. | 两组对边分别平行 | ||
| C. | 对角线互相平分 | D. | 两组对角分别相等 |
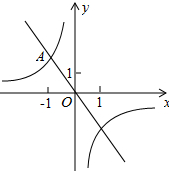 如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,n)
如图,在平面直角坐标系中,一次函数y=-2x的图象与反比例函数y=$\frac{k}{x}$的图象的一个交点为A(-1,n)
 如图,已知AB∥CD,AE∥CF,请问∠BAE和∠DCF相等吗?试说明理由.
如图,已知AB∥CD,AE∥CF,请问∠BAE和∠DCF相等吗?试说明理由.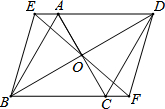 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.