题目内容
15.若去分母解分式方程$\frac{x}{x-5}$=2-$\frac{5}{5-x}$时产生增根,则增根是x=5.分析 由分式方程有增根,得到最简公分母为0,即可求出增根.
解答 解:分式方程变形得:$\frac{x}{x-5}$=2+$\frac{5}{x-5}$,
最简公分母为x-5,
由分式方程产生增根,得:x-5=0,
解得:x=5,
则增根为x=5,
故答案为:x=5
点评 此题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
6.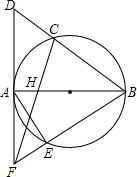 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )| A. | $\frac{8\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
10.对于反比例函数y=$\frac{2}{x}$,下列说法不正确的是( )
| A. | 当x>0时,y随x的增大而增大 | B. | 当x<0时,y随x的增大而减小 | ||
| C. | 点(-2,-1)在它的图象上 | D. | 它的图象在第一、三象限 |
20.解方程.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
(1)$\frac{10x}{2x-1}$+$\frac{5}{1-2x}$=2
(2)$\frac{1}{{x}^{2}+5x-6}$=$\frac{1}{{x}^{2}+x+6}$.
5.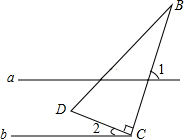 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
 如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.
如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.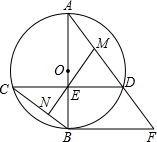 如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.
如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.