题目内容
18.在一次数学综合实践活动课上,老师用硬纸板做了两个三角形,分别为△ABC和△DEF,其中∠B=90°,∠A=45°,BC=6$\sqrt{2}$,∠F=90°,∠EDF=30°,EF=2.如图1,师生共同进行了以下的探究活动:将△ABC固定不动,并将△DEF的斜边DE与△ABC的斜边AC重合在一起,将△DEF沿AC方向移动,设△DEF在AC方向上移动的距离为x.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)①EC=8-x(用含x的代数式表示);
②如图2,连接FC,当x=6时,∠FCA=30°;
(2)将点F关于直线AC的对称点记作F′,当点F′在BC上时,求AD的长,并判断此时FC与AB的位置关系;
(3)在△DEF移动过程中,以线段AD、FC、EC的长度为三边长构造三角形,此三角形能否成为以AD长度为斜边长的直角三角形?若能,求出移动距离x,若不能,请说明理由;
(4)在△DEF沿AC方向移动的过程中,小明同学发现:F、B两点间的距离先逐渐变小,当x=3时,距离最短,此时FB=6+$\sqrt{3}$,然后F、B两点间的距离逐渐变大,小明同学由此联想到二次函数的性质,猜想F、B两点间的距离是△DEF在AC方向上移动距离x的二次函数,小明同学的猜想正确吗?不正确.(填“正确”或“不正确”,不必说明理由.)

分析 (1)根据等腰直角三角形和含30°直角三角形的性质得出AC=12,DE=4,可得EC的长度;
(2)根据对称的性质得出OF=OF′,再利用直角三角形的有关性质求出OC等边的长度,进一步分析解答即可;
(3)根据勾股定理的逆定理对直角三角形定进行判定,利用三边关系得出方程计算即可;
(4)根据当FB⊥AC时,得出距离最短进而解答即可.
解答 解:(1)①∵∠B=90°,∠A=45°,BC=6$\sqrt{2}$,
∴AC=12,
∵∠F=90°,∠EDF=30°,EF=2,
∴DE=4,
设△DEF在AC方向上移动的距离为x,
∴EC=AC-DE-x=12-4-x=8-x;
②∵∠DEF=60°,
∴∠FEC=120°,
∵∠FCA=30°,
∴∠CFE=30°,
∴EF=CE=2,
∴x=8-2=6;
(2)根据题意作出点F关于直线AC的对称点记作F′,
FF′交AC于点O,如图1:
∵FF′⊥AC,EF=2,∠F=90°,∠EDF=30°,
∴OE=1,OD=3,OF=$\sqrt{3}$,
∵FF′⊥AC,∠A=45°,OF=OF′,
∴OC=$\sqrt{3}$,
∴AD=AC-OD-OC=12-3-$\sqrt{3}$=9-$\sqrt{3}$,
此时FC∥AB.
(3)能,当以AD长度为斜边长的直角三角形,
可得AD2=x2,EC2=(8-x)2,FC2=$(\sqrt{3})^{2}+(9-x)^{2}$;
由EC2+FC2=AD2
得:x=17+$\sqrt{141}$;
(4)当FB⊥AC时,此时x=3时,距离最短,
可得:FB=6+$\sqrt{3}$;
F、B两点间的距离不是△DEF在AC方向上移动距离x的二次函数,
所以猜想不正确.
故答案为:8-x;6;3;6+$\sqrt{3}$;不正确.
点评 此题考查几何变换问题,主要利用了等腰直角三角形的性质,直角三角形30°角的性质,勾股定理,三角形的面积,综合性较强,难度较大,熟记各性质并理清各线段与AD的关系是解题的关键.

| A. | $\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | -$\sqrt{9}$=-3 | D. | -32=9 |
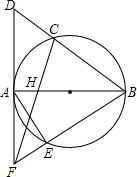 如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )
如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线AD交BC的延长线于点D,H是OA的中点,CH的延长线交切线AD于点F,BF交⊙O于点E,连接AE,若OB=2,则AE的长为( )| A. | $\frac{8\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
| A. | 当x>0时,y随x的增大而增大 | B. | 当x<0时,y随x的增大而减小 | ||
| C. | 点(-2,-1)在它的图象上 | D. | 它的图象在第一、三象限 |
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 4个 |
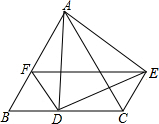 如图,已知△ABC和△ADE都是等边三角形,点D在边BC上,点E在边AD的右侧,联结CE.
如图,已知△ABC和△ADE都是等边三角形,点D在边BC上,点E在边AD的右侧,联结CE. 如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.
如图,∠1=100°,∠2=100°,∠3=110°,求∠4的度数.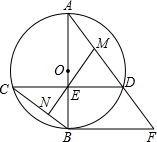 如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.
如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.