题目内容
17.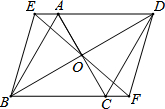 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
如图,在菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.(1)求证:四边形BFDE是平行四边形;
(2)若AB=4,CF=1,∠ABC=60°,求sin∠DEO的值.
分析 (1)由四边形ABCD是菱形,可得AD∥BC,OA=OC,OB=OD,即可证得∠AEO=∠CFO,继而证得△AOE≌△COF,则可得OE=OF,即可判定四边形BFDE是平行四边形;
(2)首先由在菱形ABCD中,∠ABC=60°,证得△ABC,△ADC为等边三角形,然后过点M作OM⊥AD于M,然后利用三角函数与勾股定理,求得OM与OE的长,则可求得答案.
解答 (1)证明:∵四边形ABCD是菱形,
∴AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AOE和△COF中,
$\left\{\begin{array}{l}{∠AEO=∠CFO}\\{∠AOE=∠COF}\\{OA=OC}\end{array}\right.$,
∴△AOE≌△COF(AAS),
∴OE=OF,
又∵OB=OD,
∴四边形BFDE是平行四边形;
(2)∵菱形ABCD,∠ABC=60°,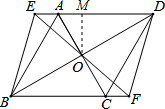
∴BD⊥AC,AB=BC=AD=CD=4,∠ADO=∠CDO=30°,
∴△ABC,△ADC为等边三角形,
∴AO=$\frac{1}{2}$AD=2,∠OAD=60°,
∴OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=2$\sqrt{3}$,
过点M作OM⊥AD于M,
∴OM=OA•sin60°=$\sqrt{3}$,
∴AM=OA•cos60°=1,
∵△AOE≌△COF,
∴AE=CF=1,
∴EM=AE+AM=2,
∴OE=$\sqrt{E{M}^{2}+O{M}^{2}}$=$\sqrt{7}$,
在Rt△EOM中,sin∠DEO=$\frac{OM}{OE}$=$\frac{\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$.
点评 此题考查了菱形的性质、平行四边形的判定与性质、等边三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.

 智能训练练测考系列答案
智能训练练测考系列答案| A. | 3个 | B. | 2个 | C. | 1个 | D. | 4个 |
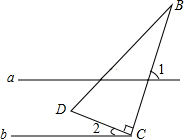 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 40° |
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $\frac{3}{2}$ |
| A. | 内角和为360° | B. | 邻角互补 | C. | 对角相等 | D. | 对角互补 |
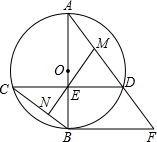 如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径.
如图,AB为⊙O的直径,且弦CD⊥AB,交点为E,过点B的切线与AD的延长线交于点F,已知cosC=$\frac{4}{5}$,BF=6,求⊙O的半径. 如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.
如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.