题目内容
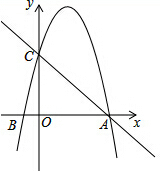 如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.
如图,抛物线y=-x2+3x+4的图象交x轴于A,B,交y轴于C,点P是抛物线的一点,若以△ACP是以AC为直角边的直角三角形,求点P的坐标.考点:抛物线与x轴的交点
专题:
分析:求出A、C坐标,从而可求出AC的解析式,再根据互相垂直的两直线比例系数之积为-1,求出PC的解析式,与抛物线组成方程组即可求出点P的坐标.
解答: 解:当y=0时,-x2+3x+4=0,解得x1=-1,x2=4.
解:当y=0时,-x2+3x+4=0,解得x1=-1,x2=4.
A点坐标为A(4,0),
C(0,4).
设AC解析式为y=kx+b,
把A(4,0),C(0,4)分别代入解析式得
,
解得
,
故解析式为y=-x+4.
(1)当CP1⊥AC时,设CP1解析式为y=x+n,
把(0,4)代入得n=4,
解析式为y=x+4,
与抛物线y=-x2+3x+4组成方程组得
,
解得
,
.
P1坐标为(2,6).
(2)当AP2⊥AC时,设AP2解析式为y=x+m,
把(4,0)代入得m=-4,
解析式为y=x-4,
与抛物线y=-x2+3x+4组成方程组得
,
解得
,
.
P2坐标为(-2,-6).
 解:当y=0时,-x2+3x+4=0,解得x1=-1,x2=4.
解:当y=0时,-x2+3x+4=0,解得x1=-1,x2=4.A点坐标为A(4,0),
C(0,4).
设AC解析式为y=kx+b,
把A(4,0),C(0,4)分别代入解析式得
|
解得
|
故解析式为y=-x+4.
(1)当CP1⊥AC时,设CP1解析式为y=x+n,
把(0,4)代入得n=4,
解析式为y=x+4,
与抛物线y=-x2+3x+4组成方程组得
|
解得
|
|
P1坐标为(2,6).
(2)当AP2⊥AC时,设AP2解析式为y=x+m,
把(4,0)代入得m=-4,
解析式为y=x-4,
与抛物线y=-x2+3x+4组成方程组得
|
解得
|
|
P2坐标为(-2,-6).
点评:本题考查了抛物线与x轴的交点,知道以下两点是解题的关键:①互相垂直的两直线比例系数之积为-1;②方程组的解是交点坐标.

练习册系列答案
相关题目
 如图,∠AOB=30°,⊙M的圆心在OA上,半径为4cm,若圆心在射线OA上移动,则当OM=
如图,∠AOB=30°,⊙M的圆心在OA上,半径为4cm,若圆心在射线OA上移动,则当OM=
 如图所示,在Rt△ABC中,∠C=90°,AC=5,BC=3,求AB和sinA.
如图所示,在Rt△ABC中,∠C=90°,AC=5,BC=3,求AB和sinA.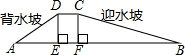 如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE=
如图是一个拦水坝的横截面示意图,坝全长为30m,坝面宽为3m,迎水坡的坡度为1:3,背水坡度为1:2,堆砌水坝用去土方2325m3,则坝高DE= 如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).
如图,已知点A的坐标为(-3,-4),点B的坐标为(5,0).