题目内容
20．
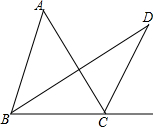如图，在△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于点D，∠D=20°，则∠A的度数是 （ ）| A． | 20° | B． | 30° | C． | 40° | D． | 50° |
分析 根据角平分线的定义和三角形的外角的性质即可得到∠D=$\frac{1}{2}$∠A，代入求出即可．
解答 解：∵∠ABC的平分线与∠ACB的外角平分线相交于D点，
∴∠1=$\frac{1}{2}$∠ACE，∠2=$\frac{1}{2}$∠ABC，
又∵∠D=∠1-∠2，∠A=∠ACE-∠ABC，
∴∠D=$\frac{1}{2}$∠A=20°．
∴∠A=40°，
故选C．
点评 此题综合考查了三角形的外角的性质以及角平分线定义的应用，解此题的关键是求出∠D=$\frac{1}{2}$∠A，难度适中．
练习册系列答案
相关题目
10．下列各组给出的三条线段中，不能组成三角形的是（ ）
| A． | 3，4，5 | B． | $\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$ | C． | 32，42，52 | D． | 2，2，1 |
8．下列命题中，是假命题的是（ ）
| A． | 成轴对称的两个图形是全等图形 | |
| B． | 直角三角形斜边上的中线等于斜边的一半 | |
| C． | 若x＞y，则x-3＞y-3 | |
| D． | ∠A的相邻外角是70°，要使△ABC为等腰三角形，则∠B为35°或110° |
5．某校初三学生开展毽子比赛活动，每班派5名学生参加，按团体总分多少排列名次，在规定时间内每踢100个（含100）为优秀．下表是成绩最好的甲班和乙班各5名学生的比赛数据（单位：个）
经统计发现两班总分相等，此时有学生建议，可以通过考查数据中的其他信息作为参考．请你回答下列问题：
（1）计算两班的优秀率及比赛数据的中位数；
（2）哪一个班级学生的比赛成绩相互之间更接近，为什么？
（3）根据以上信息，你认为应该把冠军奖状发给哪一个班级？说明理由！
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
（1）计算两班的优秀率及比赛数据的中位数；
（2）哪一个班级学生的比赛成绩相互之间更接近，为什么？
（3）根据以上信息，你认为应该把冠军奖状发给哪一个班级？说明理由！