题目内容
2.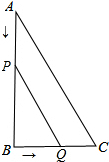 如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.
如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.(1)当P,Q的运动时间2(s)时,线段BP=18cm,线段BQ=2cm,三角形PBQ的面积S=18cm2.
(2)当P,Q的运动时间x(s)(x≤11)时,线段BP=(22-2x)cm,线段BQ=xcm,三角形PBQ的面积S=(-x2+11x)cm2;
(3)当P,Q的运动时间n(s)(n≤11)时,四边形APQC的面积y=n2-11n+110.
分析 (1)(2)利用AB的长度减去AP得出BP,运动速度乘时间得出BQ,利用三角形的面积求得三角形PBQ的面积即可;
(3)利用△ABC的面积减去三角形PBQ的面积即可得出四边形APQC的面积.
解答 解:(1)当P,Q的运动时间2(s)时,线段BP=22-2×2=18cm,线段BQ=2×1=2cm,三角形PBQ的面积S=$\frac{1}{2}$×18×2=18cm2.
(2)当P,Q的运动时间x(s)(x≤11)时,线段BP=(22-2x)cm,线段BQ=xcm,三角形PBQ的面积S=$\frac{1}{2}$(22-2x)x=(-x2+11x)cm2;
(3)当P,Q的运动时间n(s)(n≤11)时,四边形APQC的面积y=$\frac{1}{2}$×22×20-$\frac{1}{2}$(22-2n)n=(n2-11n+110)cm2.
故答案为:18cm,2cm,18cm2;(22-2x)cm,xcm,(-x2+11x)cm2;(n2-11n+110)cm2.
点评 此题考查动点函数问题,利用三角形的面积计算公式建立函数是解决问题的关键.

练习册系列答案
相关题目
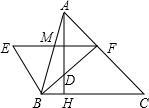 如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )
如图,△ABC中,AH⊥BC,BF平分∠ABC,BE⊥BF,EF∥BC,以下四个结论:①∠E=∠ABE;②∠ADF-∠BAH=$\frac{1}{2}$∠ABC;③∠ADF=∠AFD;④S△ABF=$\frac{FM•AH}{2}$.其中正确的有( )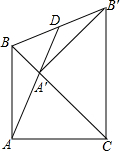 已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.
已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.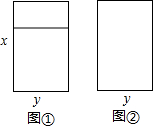 如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?
如图①,图②是宏达门窗厂制作的两种同大小的长方形铝合金窗框,已知窗框的长都是x米,窗框的宽都是y米.若王阿婆家装修需要图①窗框2个,图②窗框5个,则制作这些窗框需要铝合金多少米(接缝忽略不计)?