题目内容
7.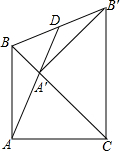 已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.
已知,在等腰三角形ABC中,AB=AC,∠BAC=90°,将△ABC绕点C旋转45°成为Rt△CA′B′,连接AA′并延长交BB′于点D,求证:BD=B′D.
分析 根据旋转的性质,△BCB'是等腰三角形,根据等腰三角形的性质即可求得∠BB'C的度数,则∠BB'A'可以求得,根据△AA'C是等腰三角形,即可求得∠AA'C的度数,则∠BA'D即可求得,进而求得∠DA'B'的度数,然后根据等角对等边即可求解.
解答 证明:将△ABC绕C点旋转45°,
又∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°.
∵点Aˊ在BC上,AC=AˊC ,
,
∴在△CAAˊ中,AC=AˊC,∠ACB=45°,
∴∠CAAˊ=∠CAˊA=67.5°,
∵在△CBBˊ中,CB=CBˊ,∠BCBˊ=45°,
∴∠CBBˊ=∠CBˊB=67.5°,
∵BC、AD相交于点Aˊ,
∴∠BAˊD=∠BAˊD=67.5°,
∴DB=DAˊ.
∵∠BAˊBˊ=90°,∠BAˊD=∠AˊBD=67.5°,
∴∠DBˊAˊ=∠DAˊBˊ=22.5°.
∴DBˊ=DAˊ,
又∵DAˊ=DB,
∴DB=DBˊ.
点评 本题考查了旋转的性质以及等腰三角新的性质,根据等腰三角形的性质求得∠BB'A'和∠DA'B'的度数是关键.

练习册系列答案
相关题目
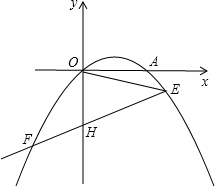 已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.
已知抛物线y=-$\frac{1}{3}$x2+$\frac{2}{3}$x经过原点,抛物线与x轴交于另一点A,点E(3,m)在抛物线上,连接OE,作∠OEF=45°,交抛物线于点F,求直线EF的解析式.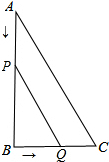 如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发.
如图,在三角形ABC中,∠B=90°,AB=22cm,BC=20cm,点P从点A出发沿AB边向点B以2cm/s的速度移动,点Q从点B出发沿BC边向点C以1cm/s的速度移动,P、Q分别从A,B同时出发. 如图,圆锥的母线长为6cm,其侧面展开图是半圆,求圆锥的底面圆的面积.
如图,圆锥的母线长为6cm,其侧面展开图是半圆,求圆锥的底面圆的面积.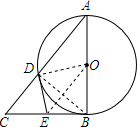 如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,DE切⊙O于D,交BC于E,求证:BE=CE.
如图,△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于D,DE切⊙O于D,交BC于E,求证:BE=CE. 如图,A、B是⊙O上的两点,∠AOB=80°,C是⊙O上不与A、B重合的任一点,求∠ACB的度数.
如图,A、B是⊙O上的两点,∠AOB=80°,C是⊙O上不与A、B重合的任一点,求∠ACB的度数.