题目内容
18．若扇形面积为3π，圆心角为60°，则该扇形的半径为（ ）| A． | 3 | B． | 9 | C． | 2$\sqrt{3}$ | D． | 3$\sqrt{2}$ |
分析 已知了扇形的圆心角和面积，可直接根据扇形的面积公式求半径长．
解答 解：扇形的面积=$\frac{60π{r}^{2}}{360}$=3π．
解得：r=3$\sqrt{2}$．
故选D．
点评 本题主要考查了扇形的面积公式=$\frac{nπ{r}^{2}}{360}$．熟练将公式变形是解题关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．
小华为参加毕业晚会演出，准备制一顶圆锥形彩色纸帽，如图所示，如果纸帽的底面半径为8cm，母线长为25cm，那么制作这顶纸帽至少需要彩色纸板的面积为200πcm2．（结果保留π）
13．若一个几何体的主视图、左视图、俯视图都是正方形，则这个几何体是（ ）
| A． | 正方体 | B． | 圆锥 | C． | 圆柱 | D． | 球 |
15．
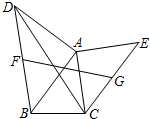如图，以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE，F、G分别是线段BD和CE的中点，则$\frac{CD}{FG}$的值等于（ ）
如图，以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE，F、G分别是线段BD和CE的中点，则$\frac{CD}{FG}$的值等于（ ）| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | $\sqrt{2}$ | C． | $\frac{3}{2}$ | D． | $\sqrt{3}$ |