题目内容
15.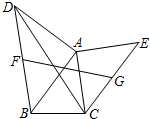 如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )
如图,以任意△ABC的边AB和AC向形外作等腰Rt△ABD和等腰Rt△ACE,F、G分别是线段BD和CE的中点,则$\frac{CD}{FG}$的值等于( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | $\sqrt{3}$ |
分析 取BC的中点H,连接BE、FH、GH,求出∠BAE=∠DAC,然后利用“边角边”证明△ABE和△ADC全等,根据全等三角形对应边相等可得BE=CD,全等三角形对应角相等可得∠ABE=∠ADC,然后求出BE⊥CD,再根据三角形的中位线平行于第三边并且等于第三边的一半可得FH∥CD且FH=$\frac{1}{2}$CD,GH∥BE且GH=$\frac{1}{2}$BE,然后求出△HFG是等腰直角三角形,根据等腰直角三角形的性质可得$\frac{FH}{FG}$=$\frac{\sqrt{2}}{2}$,然后求出$\frac{CD}{FG}$的值即可.
解答  解:如图,取BC的中点H,连接BE、FH、GH,
解:如图,取BC的中点H,连接BE、FH、GH,
∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠BAE=∠DAC,
在△ABE和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AC=AE}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴BE=CD,∠ABE=∠ADC,
∴∠BDC+∠DBE=∠BDA+∠ABD=90°,
∴BE⊥CD,
又∵F、G分别是线段BD和CE的中点,
∴FH、GH分别是△BCD和△BCE的中位线,
∴FH∥CD且FH=$\frac{1}{2}$CD,GH∥BE且GH=$\frac{1}{2}$BE,
∴△HFG是等腰直角三角形,
∴$\frac{FH}{FG}$=$\frac{\sqrt{2}}{2}$,
∴$\frac{CD}{FG}$=$\sqrt{2}$.
故选B.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰直角三角形的判断与性质,全等三角形的判断与性质,难点在于作辅助线构造出全等三角形和等腰直角三角形.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案| A. | 3 | B. | 9 | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
| 钱数目(元) | 5≤x<15 | 15≤x<25 | 25≤x<35 | 35≤x<45 | 45≤x<55 |
| 频数 | 2 | a | 20 | 14 | 3 |
| 百分比 | 0.04 | 0.22 | b | 0.28 | 0.06 |
| A. | $\frac{3}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |

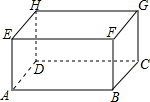 现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$.
现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$.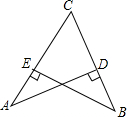 如图,从小丽家C到学校A和菜市场B的夹角∠ACB是锐角,又知道从小丽家到学校A和到菜市场B的距离相等,小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等,你认为她说得有道理吗?请说明理由.
如图,从小丽家C到学校A和菜市场B的夹角∠ACB是锐角,又知道从小丽家到学校A和到菜市场B的距离相等,小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等,你认为她说得有道理吗?请说明理由.