题目内容
9. 如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.
如图,△ABC 中,∠C=90°,AC=4,BC=8,以AB为边向外作正方形ABDE,若此正方形中心为点O,则点C和点O之间的距离为6$\sqrt{2}$.
分析 过点O作OM垂直于CA于点N,作ON垂直于CB于点N,易证四边形MCNO是矩形,利用已知条件再证明△AOM≌△BON,因为OM=ON,所以AM=BN,进而求出CN的长,根据勾股定理即可求出OC的长.
解答 解:过点O作OM垂直于CA于点N,作ON垂直于CB于点N,连接OA、OB,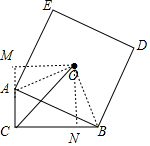
∴∠OMC=∠ONC=90°,
∵∠ACB=90°,
∴四边形MCNO是矩形,
∴∠MON=90°,
∵正方形ABDE对角线交于点O,
∴OA=OB,∠AOB=90°,
∴∠MON-∠AON=∠AOB-∠AON,
∴∠AOM=∠NOB,
∵∠OMA=∠ONB=90°,
在△AOM和△BON中,
$\left\{\begin{array}{l}{∠AOM=∠BON}\\{∠OMA=∠ONB=90°}\\{OA=OB}\end{array}\right.$,
∴△AOM≌△BON(AAS),
∴OM=ON,
∴AM=BN,
∵AC=4,BC=8,
∴CN=$\frac{AC+BC}{2}$=6,
∵∠OCN=45°,
∴ON=CN=6,
由勾股定理得OC=6$\sqrt{2}$,
故答案为:6$\sqrt{2}$.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
4.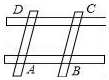 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
 如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )
如图所示是由四根木棒搭成的平行四边形框架,AB=8cm,AD=6cm,在这个位置,将AB固定,逆时针转动AD.则关于?ABCD面积S的变化描述正确的是( )| A. | 保持不变 | B. | 先变小,再变大 | C. | 先变大,再变小 | D. | 0<S<48 |
19.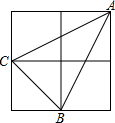 图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
 图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )
图中的大正方形是由4个小正方形组成的,小正方形边长为1,连接小正方形的三个顶点,得到△ABC,则AC边上的高为( )| A. | $\frac{3\sqrt{5}}{5}$ | B. | $\frac{4\sqrt{5}}{5}$ | C. | $\frac{5\sqrt{5}}{10}$ | D. | $\frac{3\sqrt{2}}{2}$ |
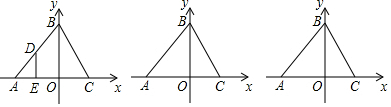
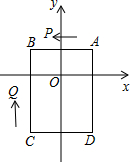 如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).
如图,已知四边形ABCD的顶点为A(1,1),B(-1,1),C(-1,-2),D(1,-2),点P从A出发同时点Q从C点出发,沿四边形的边做环绕匀速运动,P点以2单位/s的速度做逆时针运动,Q点以3单位/s的速度做顺时针运动,则点P和点Q第2017次相遇时的坐标为(0,-2).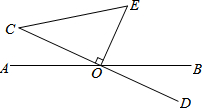 如图,AB,CD交于点O,OE⊥CD于O,连接CE,
如图,AB,CD交于点O,OE⊥CD于O,连接CE, 如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.
如图,边长为2菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°;…,按此规律所作的第4个菱形的边长为6$\sqrt{3}$.