题目内容
10．在一个不透明的纸箱内放有除颜色外无其他差别的2个红球，8个黄球和10个白球，从中随机摸出一个球为黄球的概率是$\frac{2}{5}$．分析 让黄球的个数除以球的总数即为摸到黄球的概率．
解答 解：袋子里装有2个红球，8个黄球，10个白球共20个球，从中摸出一个球是黄球的概率是$\frac{8}{20}=\frac{2}{5}$，
故答案为：$\frac{2}{5}$
点评 本题考查的是随机事件概率的求法．如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=$\frac{m}{n}$．
练习册系列答案
相关题目
1．若点A（3，-4）、B（-2，m）在同一个反比例函数的图象上，则m的值为（ ）
| A． | 6 | B． | -6 | C． | 12 | D． | -12 |
18．
如图，在△ABC中，∠A=50°，∠C=70°，则外角∠ABD的度数是（ ）
如图，在△ABC中，∠A=50°，∠C=70°，则外角∠ABD的度数是（ ）| A． | 110° | B． | 120° | C． | 130° | D． | 140° |
5．
如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（ ）
如图，在△ABC中，AB=10，AC=8，BC=12，AD⊥BC于D，点E、F分别在AB、AC边上，把△ABC沿EF折叠，使点A与点D恰好重合，则△DEF的周长是（ ）| A． | 14 | B． | 15 | C． | 16 | D． | 17 |
如图，△ABC各顶点的坐标分别是A（-2，-4），B（0，-4），C（1，-1）．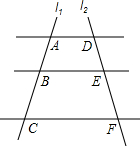
如图，AD∥BE∥CF，直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F．已知AB=1，BC=3，DE=2，则EF的长为（ ）