题目内容
13.求在直角坐标平面中不等式|x|+|y|≤3围成的图形的面积.分析 首先根据不等式写出四条直线,然后求得四条直线与坐标轴的交点,从而求得围成的图形的面积.
解答 解:这是由四条直线x+y=3,x-y=3,-x+y=3,-x-y=3围成的正方形,
与坐标轴的交点有四个:
(3,0),(-3,0),(0,3),(0,-3)
面积=$\frac{1}{2}$×6×6=18.
点评 本题考查了一次函数与一元一次不等式的知识,解题的关键是根据不等式抽象出四条直线,难度不大.

练习册系列答案
相关题目
19.“节能环保,低碳生活”是我们倡导的一种生活方式.某家电商场计划用11.8万元购进节能型电视机、洗衣机和空调共40台.三种家电的进价及售价如表所示:
(1)设购进x台电视机,若购进电视机的数量和洗衣机的数量相同,设销售总额为y元,试求出y元关于x台的函数关系式.
(2)在(1)的条件下,如果不超出现有资金,空调的数量不超过电视机数量的三倍,请问商场有哪几种进货方案?
(3)在“2013年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金购满1000元送50元家电消费券一张、多买多送”的活动,根据(2)的方案,若三种电器在活动期间全部售出,商家预计最多送出消费券多少张?
| 进价(元/台) | 售价(元/台) | |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空 调 | 2400 | 2700 |
(2)在(1)的条件下,如果不超出现有资金,空调的数量不超过电视机数量的三倍,请问商场有哪几种进货方案?
(3)在“2013年消费促进月”促销活动期间,商家针对这三种节能型产品推出“现金购满1000元送50元家电消费券一张、多买多送”的活动,根据(2)的方案,若三种电器在活动期间全部售出,商家预计最多送出消费券多少张?
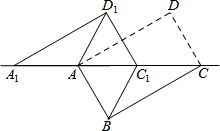 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②s=$\frac{{\sqrt{3}}}{8}{({x-2})^2}$(0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是①②④(填序号).
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②s=$\frac{{\sqrt{3}}}{8}{({x-2})^2}$(0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是①②④(填序号).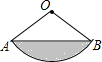 如图,∠AOB=120°,OA=2,求S阴影.
如图,∠AOB=120°,OA=2,求S阴影.
 在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么?
在六边形ABCDEF中,AF∥CD,∠A=∠D,∠B=∠E,那么BC∥EF吗?为什么?