题目内容
 如图在四边形ABCD中,AD∥BC,AC和BD相交于点O,若S△COD=3S△AOD,S△AOD=2,则S△BOC=
如图在四边形ABCD中,AD∥BC,AC和BD相交于点O,若S△COD=3S△AOD,S△AOD=2,则S△BOC=考点:相似三角形的判定与性质
专题:
分析:由S△COD=3S△AOD,可知AO:OC=1:3,又由平行可得△AOD∽△COB,再利用面积比等于相似比的平方可求得△BOC的面积.
解答:解:
∵S△COD=3S△AOD,
∴
=
,
∵AD∥BC,
∴△AOD∽△COB,
∴
=
,即
=
,
∴S△BOC=18,
故答案为:18.
∵S△COD=3S△AOD,
∴
| AO |
| CO |
| 1 |
| 3 |
∵AD∥BC,
∴△AOD∽△COB,
∴
| S△AOD |
| S△COB |
| 1 |
| 9 |
| 2 |
| S△BOC |
| 1 |
| 9 |
∴S△BOC=18,
故答案为:18.
点评:本题主要考查相似三角形的判定和性质,由条件得到
=
是解题的关键.
| AO |
| CO |
| 1 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 AB为⊙O的直径,弦CD⊥AB,垂足为E,下列结论中错误的是( )
AB为⊙O的直径,弦CD⊥AB,垂足为E,下列结论中错误的是( )| A、CE=DE | ||||
B、
| ||||
| C、∠BAC=∠BAD | ||||
| D、AC=ED |
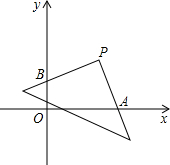 如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是
如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是 如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BD=CE,BE=CF,如果点G为DF的中点,那么EG与DF垂直吗?
如图,在△ABC中,AB=AC,点D,E,F分别在边AB,BC,AC上,且BD=CE,BE=CF,如果点G为DF的中点,那么EG与DF垂直吗?
 小明从A地出发,水平向右走100m后向左转20°,再沿直线前进100m,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走了
小明从A地出发,水平向右走100m后向左转20°,再沿直线前进100m,又向左转20°,…,照这样走下去,他第一次回到出发地A点时,一共走了