题目内容
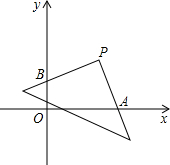 如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是
如图,在平面平角坐标系中,将直角三角形顶点放在P(4,4)处,两直角边与坐标轴交点分别为A,B.则OA+OB的长是考点:全等三角形的判定与性质,坐标与图形性质
专题:
分析:作PD⊥OB,PE⊥OA,易证△AEP≌△BDP,可得BD=AE,即可求得OA+OB=OD+OE,即可解题.
解答:解:作PD⊥OB,PE⊥OA,
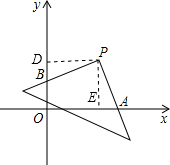
∴OD=OE=PD=PE=4,
∵∠DPB+∠BPE=90°,∠APE+∠BPE=90°,
∴∠DPB=∠APE,
∵在△AEP和△BDP中,
,
∴△AEP≌△BDP,(ASA)
∴BD=AE,
∴OB+OA=OB+OE+EA=OB+BD+OE=OD+OE;
∴OA+OB=8.

∴OD=OE=PD=PE=4,
∵∠DPB+∠BPE=90°,∠APE+∠BPE=90°,
∴∠DPB=∠APE,
∵在△AEP和△BDP中,
|
∴△AEP≌△BDP,(ASA)
∴BD=AE,
∴OB+OA=OB+OE+EA=OB+BD+OE=OD+OE;
∴OA+OB=8.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEP≌△BDP是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长.
如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,求AE的长. 如图在四边形ABCD中,AD∥BC,AC和BD相交于点O,若S△COD=3S△AOD,S△AOD=2,则S△BOC=
如图在四边形ABCD中,AD∥BC,AC和BD相交于点O,若S△COD=3S△AOD,S△AOD=2,则S△BOC= 如图,F为⊙O的直径BA延长线上一点,FC切⊙O于点C,CD⊥AB交于点D,E为
如图,F为⊙O的直径BA延长线上一点,FC切⊙O于点C,CD⊥AB交于点D,E为
 在直线l上顺次取A、B、C、D四点(如图所示)问:
在直线l上顺次取A、B、C、D四点(如图所示)问: 如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=
如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=