题目内容
16.某玩具商计划生产A、B两种型号的玩具投入市场,初期计划生产100件,生产投入资金不少于22400元,但不超过22500元,且资金要全部投入到生产这两种型号的玩具.假设生产的这两种型号玩具能全部售出,这两种玩具的生产成本和售价如表:| 型号 | A | B |
| 成本(元) | 200 | 240 |
| 售价(元) | 250 | 300 |
(2)该玩具商如何生产,就能获得最大利润?
分析 (1)设该厂生产A型玩具x件,则生产B型玩具100-x件,由题意可得:22400≤200x+240(100-x)≤22500,求解即得;
(2)计算出各种生产方案所获得的利润即得最大利润方案.
解答 解:(1)设该厂生产A型玩具x件,则生产B型玩具(100-x)件,
由“该厂所筹生产资金不少于22400万元,但不超过22500万元”和表中生产成本可得:
22400≤200x+240(100-x)≤22500,
37.5≤x≤40,
∵x为整数,
∴x取值为38、39、40.
故有三种生产方案.
即:第一种方案:生产A型号玩具38件,生产B号玩具62件;
第二种方案:生产A号玩具39件,生产B号玩具61件;
第三种方案:生产A号玩具40件,生产B号玩具60件.
(2)三种方案获得的利润分别为:
第一种方案:38×(250-200)+62×(300-240)=5620;
第二种方案:39×(250-200)+61×(300-240)=5610;
第三种方案:40×(250-200)+60×(300-240)=5600.
故生产A号玩具38台,生产B号玩具62台的方案获得利润最大.
点评 本题考查了一次函数的应用一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
11.下列计算正确的是( )
| A. | x7÷x4=x11 | B. | (a3)2=a5 | C. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | D. | $\sqrt{6}$÷$\sqrt{3}$=$\sqrt{2}$ |
9.在平面直角坐标系中,点A(5,-4)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,河堤横断面迎水坡AB的坡度是1:2,堤高BC=5m,则坡面AB的长度是5$\sqrt{5}$m.
如图,河堤横断面迎水坡AB的坡度是1:2,堤高BC=5m,则坡面AB的长度是5$\sqrt{5}$m.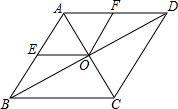 如图,E、F分别是菱形ABCD的边AB、AD的中点,且AB=5,AC=6.
如图,E、F分别是菱形ABCD的边AB、AD的中点,且AB=5,AC=6.