题目内容
4．-$\sqrt{5}$的绝对值是$\sqrt{5}$，$\frac{1}{16}$的算术平方根是$\frac{1}{4}$．分析 根据负数的绝对值等于它的相反数进行计算；根据算术平方根的定义进行解答．
解答 解：-$\sqrt{5}$的绝对值是$\sqrt{5}$，$\frac{1}{16}$的算术平方根是$\frac{1}{4}$，
故答案为：$\sqrt{5}$；$\frac{1}{4}$
点评 本题考查了算术平方根的定义、绝对值的定义．注意一个正数的算术平方根是正数，0的算术平方根是0；负数没有算术平方根．
练习册系列答案
相关题目
12．用配方法解方程x2+10x+9=0，配方后可得（ ）
| A． | （x+5）2=16 | B． | （x+5）2=1 | C． | （x+10）2=91 | D． | （x+10）2=109 |
9．在一个不透明的袋子中装有红白两种颜色的球（形状大小质地完全相同）共25个，其中白球有5个．每次从中随机摸出一个球，并记下颜色后放回，那么从袋子中随机摸出一个红球的概率是$\frac{4}{5}$．
16．某玩具商计划生产A、B两种型号的玩具投入市场，初期计划生产100件，生产投入资金不少于22400元，但不超过22500元，且资金要全部投入到生产这两种型号的玩具．假设生产的这两种型号玩具能全部售出，这两种玩具的生产成本和售价如表：
（1）该玩具商对这两种型号玩具有哪几种生产方案？
（2）该玩具商如何生产，就能获得最大利润？
| 型号 | A | B |
| 成本（元） | 200 | 240 |
| 售价（元） | 250 | 300 |
（2）该玩具商如何生产，就能获得最大利润？
17．
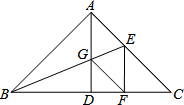如图，AD为等腰直角三角形ABC斜边BC的中线，折叠△ABC，使AB落在BC上，点A恰好与BC上的点F重合，展开后，折痕BE分别交AC、AD于点E、G，连接GF．有下列四个结论：
①AE=AG；②AE∥GF；③$\frac{AG}{GD}=\sqrt{2}$；④3S△BGD=S△BEF
其中正确结论为（ ）
如图，AD为等腰直角三角形ABC斜边BC的中线，折叠△ABC，使AB落在BC上，点A恰好与BC上的点F重合，展开后，折痕BE分别交AC、AD于点E、G，连接GF．有下列四个结论：①AE=AG；②AE∥GF；③$\frac{AG}{GD}=\sqrt{2}$；④3S△BGD=S△BEF
其中正确结论为（ ）
| A． | ②③④ | B． | ①③④ | C． | ①②③ | D． | ①②④ |
18．下列事件是随机事件的是（ ）
| A． | 漳州市在六月份下了雪 | B． | 太阳从东边升起 | ||
| C． | 打开电视机正在播动画片 | D． | 两个奇数之和为偶数 |