题目内容
如图，AB∥EF∥CD，∠ABC=45°，∠CEF=155°，则∠BCE等于（ ）| A、10° | B、15° |
| C、20° | D、25° |
考点：平行线的性质
专题：
分析：根据平行线的性质得到∠BCD=∠ABC=45°，∠FEC+∠ECD=180，求出∠ECD，根据∠BCE=∠BCD-∠ECD求出即可．
解答：解：∵AB∥EF∥CD，∠ABC=45°，∠CEF=155°，
∴∠BCD=∠ABC=45°，∠FEC+∠ECD=180°，
∴∠ECD=180°-∠FEC=25°，
∴∠BCE=∠BCD-∠ECD=45°-25°=20°．
故选：C．
∴∠BCD=∠ABC=45°，∠FEC+∠ECD=180°，
∴∠ECD=180°-∠FEC=25°，
∴∠BCE=∠BCD-∠ECD=45°-25°=20°．
故选：C．
点评：本题主要考查对平行线的性质的理解和掌握，能熟练地运用平行线的性质进行计算是解此题的关键．
练习册系列答案
相关题目
根据图形，回答问题．已知xa=3，xb=5，则x4a-3b=（ ）
| A、-44 | ||
B、
| ||
C、
| ||
D、
|
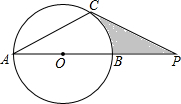如图，⊙O的半径为4，PC切⊙O于点C，交直径AB延长线于点P，若CP长为4，则阴影部分的面积为（ ）| A、8-2π | B、8-π |
| C、16-2π | D、16-π |
如图，已知△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S1，S2，S3分别表示这三个正方形的面积，S1=81，S2=225，则S3=（ ）
如图，利用一面长为34米的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏）设矩形ABCD的边AD长为x米，AB长为y米，矩形的面积为S平方米，且x＜y．