题目内容
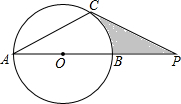 如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为( )
如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为( )| A、8-2π | B、8-π |
| C、16-2π | D、16-π |
考点:切线的性质,扇形面积的计算
专题:计算题
分析:连结OC,根据切线的性质得∠OCP=90°,由于CO=4,CP=4,可判断△CPO为等腰直角三角形,所以∠COP=45°,然后根据扇形面积公式和阴影部分的面积=S△OCP-S扇形OCB进行计算即可.
解答:解: 连结OC,如图,
连结OC,如图,
∵PC切⊙O于点C,
∴OC⊥CP,
∴∠OCP=90°,
∵CO=4,CP=4,
∴△CPO为等腰直角三角形,
∴∠COP=45°,
∴阴影部分的面积=S△OCP-S扇形OCB
=
×4×4-
=8-2π.
故选A.
 连结OC,如图,
连结OC,如图,∵PC切⊙O于点C,
∴OC⊥CP,
∴∠OCP=90°,
∵CO=4,CP=4,
∴△CPO为等腰直角三角形,
∴∠COP=45°,
∴阴影部分的面积=S△OCP-S扇形OCB
=
| 1 |
| 2 |
| 45•π•42 |
| 360 |
=8-2π.
故选A.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了扇形的面积公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=
如图,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=| 1 |
| 2 |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
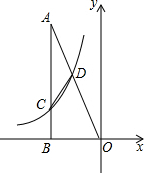 如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )
如图,Rt△ABO中,∠ABO=90°,AC=3BC,D为OA中点,反比例函数经过C、D两点,若△ACD的面积为3,则反比例函数的解析式为( )A、y=
| ||
B、y=-
| ||
C、y=
| ||
D、y=-
|
 如图,AB∥EF∥CD,∠ABC=45°,∠CEF=155°,则∠BCE等于( )
如图,AB∥EF∥CD,∠ABC=45°,∠CEF=155°,则∠BCE等于( )| A、10° | B、15° |
| C、20° | D、25° |
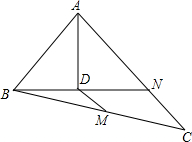 如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM=
如图,在△ABC中,∠BAC=90°,AB=6,AC=8,N是AC上的点,且AN=AB,连接BN,作AD⊥BN于D,点M是BC上的动点,则当BM=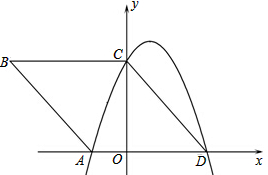 如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数
如图,在直角坐标系中,菱形ABCD的顶点A、C、D在坐标轴上,二次函数 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线