题目内容
3.等腰三角形的腰长为10,底长为12,则其底边上的中线长为( )| A. | 64 | B. | 25 | C. | 13 | D. | 8 |
分析 在等腰三角形的腰和底边高线所构成的直角三角形中,根据勾股定理即可求得底边上高线的长度.
解答  解:如图:AB=AC=10,BC=12.
解:如图:AB=AC=10,BC=12.
∵△ABC中,AB=AC,AD⊥BC,BD=CD;
则BD=DC=$\frac{1}{2}$BC=6;
Rt△ABD中,AB=10cm,BD=6;
由勾股定理,得:AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=8.
故选:D.
点评 本题考查了等腰三角形底边上高的性质和勾股定理,等腰三角形底边上的高所在直线为底边的中垂线.然后根据勾股定理即可求出底边上高的长度.

练习册系列答案
相关题目
14.若a2+a-1=0,则a3+2a2+2016的值为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
18.下列分式是最简分式的是( )
| A. | $\frac{4}{2x}$ | B. | $\frac{x-1}{{{x^2}-1}}$ | C. | $\frac{2x}{{{x^2}+1}}$ | D. | $\frac{1-x}{x-1}$ |
8.下列比较大小正确的是( )
| A. | -12>-11 | B. | |-6|=-(-6) | C. | -(-31)<+(-31) | D. | -$\frac{1}{16}$>0 |
15.能清楚地表示出各部分在总体中所占百分比的统计图是( )
| A. | 条形统计图 | B. | 扇形统计图 | C. | 折线统计图 | D. | 都可以 |
12.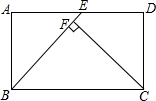 如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )
如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )
 如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )
如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )| A. | $\frac{12}{5}$ | B. | 4 | C. | 5 | D. | $\frac{24}{5}$ |
13.下列各组线段的长度成比例的是( )
| A. | 2cm,3cm,4cm,5cm | B. | 1cm,$\sqrt{2}$cm,2cm,$\sqrt{2}$cm | ||
| C. | 1.5cm,2.5cm,4.5cm,6.5cm | D. | 1.1cm,2.2cm,3.3cm,4.4cm |
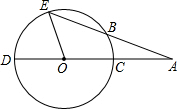 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.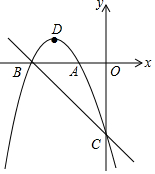 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(-3,0)两点,与y轴交于点C.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(-3,0)两点,与y轴交于点C.