题目内容
12.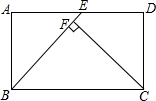 如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )
如图,矩形ABCD中,AB=4,BC=6,点E是AD的中点,CF⊥BE于点F,则CF=( )| A. | $\frac{12}{5}$ | B. | 4 | C. | 5 | D. | $\frac{24}{5}$ |
分析 根据矩形的性质得出AD∥BC,∠A=90°,证明△ABE∽△FCB,由相似三角形的判定与性质得出比例式,进而得出答案.
解答 解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∴∠AEB=∠CBF,
∵∠A=90°,∠CFB=90°,
∴△ABE∽△FCB,
∴$\frac{AB}{FC}=\frac{BE}{BC}$,
∵AB=4,BC=6,E是AD的中点,
∴AE=3,
∴BE=$\sqrt{A{B}^{2}+A{E}^{2}}$=5,
∴$\frac{4}{FC}=\frac{5}{6}$,
解得:FC=$\frac{24}{5}$.
故选:D.
点评 此题主要考查了矩形的性质、勾股定理、相似三角形的判定与性质,根据已知得出△ABE∽△FCB是解题关键.

练习册系列答案
相关题目
2.下列安全标志图中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.等腰三角形的腰长为10,底长为12,则其底边上的中线长为( )
| A. | 64 | B. | 25 | C. | 13 | D. | 8 |
20.下列各数:$\sqrt{2}$,1.414,-$\frac{1}{3}$,0.其中是无理数的为( )
| A. | $\sqrt{2}$ | B. | 1.414 | C. | -$\frac{1}{3}$ | D. | 0 |
7.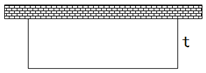 有长为l的篱笆,利用他和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )
有长为l的篱笆,利用他和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )
 有长为l的篱笆,利用他和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )
有长为l的篱笆,利用他和房屋的一面墙围成如图形状的长方形园子,园子的宽为t,则所围成的园子面积为( )| A. | (l-$\frac{t}{2}$)t | B. | (l-t)t | C. | ($\frac{l}{2}$-t)t | D. | (l-2t)t |
17.如果支出15元记作-15元,那么收入20元记作( )
| A. | +5元 | B. | +20元 | C. | -5元 | D. | -20元 |
4.有x支球队参加篮球比赛,共比赛了45场,每两队之间都比赛一场,则下列方程中符合题意的是( )
| A. | $\frac{1}{2}$ x(x-1)=45 | B. | $\frac{1}{2}$ x(x+1)=45 | C. | x(x-1)=45 | D. | x(x+1)=45 |
1.若一组数据:2,-1,x,3的极差是5,则x的值为( )
| A. | 6 | B. | -2 | C. | 4 | D. | 4或-2 |
2. 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
 如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )
如图所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=( )| A. | 55° | B. | 50° | C. | 45° | D. | 60° |