题目内容
13.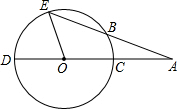 如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
如图,CD是⊙O的直径,∠EOD=72°,AE交⊙O于点B,且AB=OC,则∠A=24°.
分析 首先设∠A=x°,由AB=OC,可得AB=OB=OE,然后利用等腰三角形的性质与三角形外角的性质,求得∠EOD=3x°,继而求得答案.
解答 解:设∠A=x°,
∵AB=OC,OC=OB,
∴AB=OB,
∴∠AOB=∠A=x°,
∴∠OBE=∠A+∠AOB=2x°,
∵OB=OE,
∴∠E=∠OBE=2x°,
∴∠EOD=∠A+∠E=3x°=72°,
∴∠A=24°.
故答案为:24°.
点评 此题考查了等腰三角形的性质以及三角形外角的性质.注意设∠A=x°,利用方程思想求解是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知一元二次方程x2-5x+3=0的两根为x1,x2,则x1x2=( )
| A. | 5 | B. | -5 | C. | 3 | D. | -3 |
2.下列安全标志图中,是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.等腰三角形的腰长为10,底长为12,则其底边上的中线长为( )
| A. | 64 | B. | 25 | C. | 13 | D. | 8 |
 如图,在△ABC中,∠C=90°,∠A=30°,点D,E分别在AC,AB边上,沿DE折叠使点A落在BC上的点F处,且EF⊥BC,BE=4,则CF=$\sqrt{3}$.
如图,在△ABC中,∠C=90°,∠A=30°,点D,E分别在AC,AB边上,沿DE折叠使点A落在BC上的点F处,且EF⊥BC,BE=4,则CF=$\sqrt{3}$.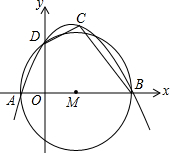 如图,⊙M的圆心M在x轴上,且与x轴分别交于A、B两点与y轴的正半轴交于点D,点A、B的横坐标分别是方程x2=3x+4的两根,一条抛物线经过A、B、D三点,点C为第一象限抛物线上一动点.
如图,⊙M的圆心M在x轴上,且与x轴分别交于A、B两点与y轴的正半轴交于点D,点A、B的横坐标分别是方程x2=3x+4的两根,一条抛物线经过A、B、D三点,点C为第一象限抛物线上一动点.