题目内容
12．
如图，已知直线y=kx-3经过点M，求此直线上（1）横坐标为2的点；
（2）横坐标为3的点；
（3）到y轴的距离等于2的点．
分析 把M点坐标代入y=kx-3求出k即可得到直线解析式；
（1）计算自变量为2时的函数值即可；
（2）计算自变量为3时的函数值即可；
（3）由题设和（1）的结论写出横坐标为-2或2的点即可．
解答 解：把M（-2，1）代入y=kx-3得-2k-3=-1，解得k=-1，
所以直线解析式为y=-x-3，
（1）当x=2时，y=-2-3=-5，
所以横坐标为2的点为（2，-5）；
（2）当x=3时，y=-3-3=-6，
所以横坐标为2的点为（3，-6）；
（3）到y轴的距离等于2的点为（-2，1）或（2，-5）．
点评 本题考查了一次函数图象上点的坐标特征：一次函数y=kx+b，（k≠0，且k，b为常数）的图象是一条直线．它与x轴的交点坐标是（-$\frac{b}{k}$，0）；与y轴的交点坐标是（0，b）．直线上任意一点的坐标都满足函数关系式y=kx+b．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
2．将数32507取近似值时，保留2个有效数字正确的是（ ）
| A． | 32 | B． | 33 | C． | 33000 | D． | 3.3×104 |
3．
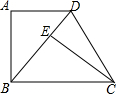如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•
（1）求证：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度数；
（3）若AD=3，AB=4，求DC的长．
如图，在四边形ABCD中，AD∥BC，∠A=90°，CE⊥BD于E，AB=EC•（1）求证：△ABD≌△ECB；
（2）若∠EDC=65°，求∠ECB的度数；
（3）若AD=3，AB=4，求DC的长．
一次函数y=kx+b（k、b为常数，且k≠0）的图象如图所示．根据图象信息可求得关于x的方程kx+b=-3的解为x=-4．
7．对二次函数y=3x2-6x的图象性质，下列说法不正确的是（ ）
| A． | 开口向上 | B． | 对称轴为x=1 | C． | 顶点坐标为（1，-3） | D． | 最小值为3 |