题目内容
14.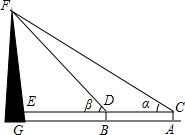 如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
如图,为了测量合浦文昌塔的高度,某校兴趣小组在塔前的平地A处安装了测角仪,测得塔顶的仰角∠α=30°,又沿着塔的方向前进25米到达B处测量,测得塔顶的仰角∠β=45°,已知测角仪的高AC=1.5米,请你根据上述数据,计算塔FG的高度(结果精确到0.1米).
分析 设EF=x米,在Rt△FDE中,∠FDE=∠DFE=45°,可得出DE=EF,CE=x+25,在Rt△CEF中利用锐角三角函数的定义即可求出x的值,进而可得出结论.
解答 解:设EF=x米,
在Rt△FDE中,
∵∠FDE=∠DFE=45°,
∴DE=EF=x米,
∴CE=(x+25)米,
Rt△CEF中,
∵∠FCE=30°,
∴$\frac{EF}{CE}$=tan∠C=$\frac{\sqrt{3}}{3}$,
∴$\frac{x}{x+25}$=$\frac{\sqrt{3}}{3}$,
解得:x=$\frac{25}{2}$($\sqrt{3}$+1)米,
∴FG=EF+EG=EF+AC=$\frac{25}{2}$($\sqrt{3}$+1)+1.5≈35.7(米).
答:古塔的高约为35.7米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
5.顺次连结矩形四边的中点所得的四边形是( )
| A. | 矩形 | B. | 正方形 | C. | 菱形 | D. | 以上都不对 |
2.将数32507取近似值时,保留2个有效数字正确的是( )
| A. | 32 | B. | 33 | C. | 33000 | D. | 3.3×104 |
 如图,已知△ABC中BC=3cm,AC=4cm,AB=5cm,将△ABC绕AC旋转一周得到的几何体的侧面积为15π.
如图,已知△ABC中BC=3cm,AC=4cm,AB=5cm,将△ABC绕AC旋转一周得到的几何体的侧面积为15π.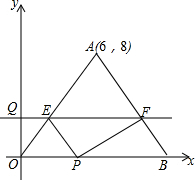 如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).
如图,等腰三角形OAB的一边OB在x轴的正半轴上,点A的坐标为(6,8),OA=OB,动点P从原点O出发,在线段OB上以每秒2个单位的速度向点B匀速运动,动点Q从原点O出发,沿y轴的正半轴以每秒1个单位的速度向上匀速运动,过点Q作x轴的平行线分别交OA,AB于E,F,设动点P,Q同时出发,当点P到达点B时,点Q也停止运动,他们运动的时间为t秒(t≥0).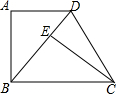 如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•
如图,在四边形ABCD中,AD∥BC,∠A=90°,CE⊥BD于E,AB=EC•