题目内容
12. 如图所示是函数y=-$\frac{3}{4}$x+3的图象,那么方程-$\frac{3}{4}$x+3=0的解是x=4,不等式-$\frac{3}{4}$x+3<0的解集是x>4,当y>3时,x的取值范围是x<0.
如图所示是函数y=-$\frac{3}{4}$x+3的图象,那么方程-$\frac{3}{4}$x+3=0的解是x=4,不等式-$\frac{3}{4}$x+3<0的解集是x>4,当y>3时,x的取值范围是x<0.
分析 函数y=-$\frac{3}{4}$x+3图象与x轴交点的横坐标的值即为方程-$\frac{3}{4}$x+3=0的解;函数y=-$\frac{3}{4}$x+3图象在x轴下方的部分对应的x的取值范围就是不等式-$\frac{3}{4}$x+3<0的解集;
由图象可知,y=3时,x=0,再根据函数的增减性即可求出当y>3时x的取值范围.
解答 解:∵函数y=-$\frac{3}{4}$x+3过点(4,0),
∴方程-$\frac{3}{4}$x+3=0的解是x=4;
∵当x>4时,函数y=-$\frac{3}{4}$x+3图象在x轴下方,即y<0,
∴不等式-$\frac{3}{4}$x+3<0的解集是x>4;
∵函数y=-$\frac{3}{4}$x+3过点(0,3),且y随x的增大而减小,
∴当y>3时,x的取值范围是x<0.
故答案为:x=4,x>4,x<0.
点评 此题主要考查了一次函数与一元一次方程、一次函数与一元一次不等式的关系,关键是正确从图象中得到信息.

练习册系列答案
相关题目
4. 如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
 如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )
如图,在△ABC中,∠A=90°,点D在AC边上,DE∥BC,若∠1=155°,则∠B的度数为( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
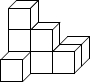 如图是由八个相同的小正方体组合而成的几何体,其俯视图是 ( )
如图是由八个相同的小正方体组合而成的几何体,其俯视图是 ( )