题目内容
13．
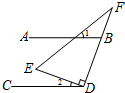如图，直线AB∥CD，Rt△DEF如图放置，∠EDF=90°，若∠1+∠F=70°，则∠2的度数为（ ）| A． | 20° | B． | 25° | C． | 30° | D． | 40° |
分析 先由外角的性质可得：∠ABD=∠1+∠F=70°，然后由两直线平行同内角互补可得：∠ABD+∠BDC=180°，进而可得：∠BDC=110°，然后由∠EDF=90°，进而即可求得∠2的度数．
解答 解：∵AB∥CD，
∴∠ABD+∠BDC=180°，
∵∠ABD=∠1+∠F=70°，
∴∠BDC=110°，
∵∠EDF=90°，
∴∠2=∠BDC-∠EDF=20°．
故答案为：A．
点评 此题考查了平行线的性质，解题的关键是：熟记两直线平行同位角相等，两直线平行内错角相等，两直线平行同旁内角互补．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
4．
如图，在△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=155°，则∠B的度数为（ ）
如图，在△ABC中，∠A=90°，点D在AC边上，DE∥BC，若∠1=155°，则∠B的度数为（ ）| A． | 45° | B． | 55° | C． | 65° | D． | 75° |
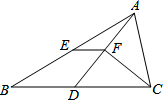已知：如图，在△ABC中，点D为BC上一点，CA=CD，CF平分∠ACB，交AD于点F，点E为AB的中点．若EF=2，则BD=4．