题目内容
7.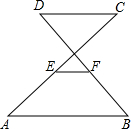 如图,AB∥CD,E、F分别为AC、BD的中点,若AB=7,CD=4,则EF的长是$\frac{3}{2}$.
如图,AB∥CD,E、F分别为AC、BD的中点,若AB=7,CD=4,则EF的长是$\frac{3}{2}$.
分析 首先连接CF,并延长交AB于点G,易证得△CDF≌△GBF(ASA),即可求得CF=GF,CD=GB=4,继而可得EF是△ACG的中位线,则可求得答案.
解答  解:连接CF,并延长交AB于点G,
解:连接CF,并延长交AB于点G,
∵AB∥CD,
∴∠CDF=∠GBF,
在△CDF和△GBF中,
$\left\{\begin{array}{l}{∠CDF=∠GBF}\\{DF=BF}\\{∠DFC=∠BFG}\end{array}\right.$,
∴△CDF≌△GBF(ASA),
∴CF=GF,CD=GB=4,
∴AG=AB-BG=7-4=3,
又∵E为AC的中点,
∴EF是△ACG的中位线,
∴EF=$\frac{1}{2}$AG=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了梯形的性质、全等三角形的判定与性质以及三角形的中位线的性质.注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
18.某下岗职工购进一批货物,到集贸市场零售,已知卖出去的货物数量x与售价y的关系如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当货物数量时5kg的时候,售价是多少元?
(3)如果售价是(27+0.9)元,那么货物数量是多少千克?
(4)你能尝试着写出卖出去的售价y与货物数量x的之间的关系式吗?
| 数量x(千克) | 1 | 2 | 3 | 4 | 5 |
| 售价y(元) | 3+0.1 | 6+0.2 | 9+0.3 | 12+0.4 | 15+0.5 |
(2)当货物数量时5kg的时候,售价是多少元?
(3)如果售价是(27+0.9)元,那么货物数量是多少千克?
(4)你能尝试着写出卖出去的售价y与货物数量x的之间的关系式吗?
16.下列方程有解的是( )
| A. | x-1=1-x | B. | x+4=x-4 | C. | |x+1|+1=0 | D. | 2(x+2)=2x |
17.已知x轴上一点A(6,0),y轴上一点B(0,b),且AB=10,则b的值为( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上答案都不对 |
 张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.
张师傅要在如图所示的钝角三角形铁片上截取一个面积最大的半圆形工件,如果要求半圆形工件的直径恰好在三角形铁片的最长边上.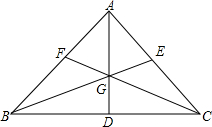 如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?
如图在△ABC中,点D、E、F分别在三边上,E是AC中点.AD、BE、CF交于点G,BD=2DC,S△GCE=4,S△GCD=5,求△ABC的面积?