题目内容
 如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.
如图:⊙O1和⊙O2是等圆,外切于点A,过点A的直线交⊙O1于B点,交⊙O2于点C,求证:AB=AC.考点:相切两圆的性质
专题:证明题
分析:如图,作辅助线;证明△AO1B≌△AO2C,得到AB=AC即可解决问题.
解答:
 解:如图,过点A作两圆的公切线MN;
解:如图,过点A作两圆的公切线MN;
连接O1B、O2C、O1O2,而两圆外切,
∴O1O2必过切点A;
∵∠AO1B=2∠NAB,∠AO2C=2∠MAC,
且∠NAB=∠MAC,
∴∠AO1B=∠AO2C;
在△AO1B与△AO2C中,
,
∴△AO1B≌△AO2C(SAS),
∴AB=AC.
 解:如图,过点A作两圆的公切线MN;
解:如图,过点A作两圆的公切线MN;连接O1B、O2C、O1O2,而两圆外切,
∴O1O2必过切点A;
∵∠AO1B=2∠NAB,∠AO2C=2∠MAC,
且∠NAB=∠MAC,
∴∠AO1B=∠AO2C;
在△AO1B与△AO2C中,
|
∴△AO1B≌△AO2C(SAS),
∴AB=AC.
点评:该题主要考查了相切两圆的性质及其应用问题;解题的关键是作辅助线,构造全等三角形.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+
如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,按如图所示的直角坐标系,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=-x2+2x+ 如图,边长为a的正六边形内有两个三角形(数据如图),则
如图,边长为a的正六边形内有两个三角形(数据如图),则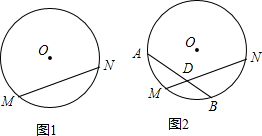 如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.
如图1,已知⊙O的弦MN所对的弧是120°,圆心O到MN所在的直线的距离是4.