题目内容
11．若a2-5ab+4b2=0，$\frac{2a+3b}{5b}$=1或$\frac{11}{5}$．分析 根据因式分解求得a=b，a=4b，代入$\frac{2a+3b}{5b}$求解即可．
解答 解：∵a2-5ab+4b2=0，
∴（a-b）（a-4b）=0，
∴a=b，a=4b，
当a=b时，$\frac{2a+3b}{5b}$=$\frac{2b+3b}{5b}$=1；
当a=4b时，$\frac{2a+3b}{5b}$=$\frac{8b+3b}{5b}$=$\frac{11b}{5b}$=$\frac{11}{5}$；
故答案为：1或$\frac{11}{5}$．
点评 本题考查了因式分解法解一元二次方程和求代数式的值．根据因式分解得出a，b的关系是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，点D是△ABC内一点，连接BD、CD．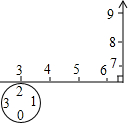
如图所示，数轴被折成90°，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字2所对应的点与数轴上的数3所对应的点重合，数轴固定，圆紧贴数轴沿着数轴的正方向滚动，那么数轴上的数2013将与圆周上的数字0重合．
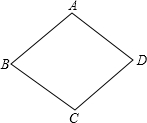如图，已知菱形ABCD，画一个矩形，使得A，B，C，D四点分别在矩形的四条边上，且矩形的面积为菱形ABCD面积的2倍．
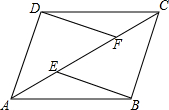如图，在四边形ABCD中，BE=DF．