题目内容
9．已知x1，x2是方程x2-5x+$\sqrt{3}$=0的两根，求（x1+1）（x2+1）的值．分析 根据根与系数的关系得到x1+x2=5，x1x2=$\sqrt{3}$，再利用多项式乘法把（x1+1）（x2+1）展开得到x1x2+x1+x2+1，然后利用整体代入的方法计算．
解答 解：根据题意得x1+x2=5，x1x2=$\sqrt{3}$，
所以（x1+1）（x2+1）=x1x2+x1+x2+1=$\sqrt{3}$+5+1=$\sqrt{3}$+6．
点评 本题考查了根与系数的关系：若x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时，x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
相关题目
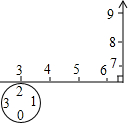如图所示，数轴被折成90°，圆的周长为4个单位长度，在圆的4等分点处标上数字0，1，2，3，先让圆周上数字2所对应的点与数轴上的数3所对应的点重合，数轴固定，圆紧贴数轴沿着数轴的正方向滚动，那么数轴上的数2013将与圆周上的数字0重合．
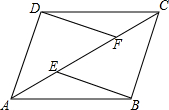如图，在四边形ABCD中，BE=DF．