题目内容
9.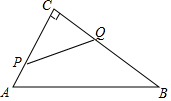 如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )| A. | 19cm2 | B. | 16cm2 | C. | 15cm2 | D. | 12cm2 |
分析 在Rt△ABC中,利用勾股定理可得出AC=6cm,设运动时间为t(0≤t≤4),则PC=(6-t)cm,CQ=2tcm,利用分割图形求面积法可得出S四边形PABQ=t2-6t+24,利用配方法即可求出四边形PABQ的面积最小值,此题得解.
解答 解:在Rt△ABC中,∠C=90°,AB=10cm,BC=8cm,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6cm.
设运动时间为t(0≤t≤4),则PC=(6-t)cm,CQ=2tcm,
∴S四边形PABQ=S△ABC-S△CPQ=$\frac{1}{2}$AC•BC-$\frac{1}{2}$PC•CQ=$\frac{1}{2}$×6×8-$\frac{1}{2}$(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.
故选C.
点评 本题考查了二次函数的最值以及勾股定理,利用分割图形求面积法找出S四边形PABQ=t2-6t+24是解题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
20.下列各式计算正确的是( )
| A. | a2+2a3=3a5 | B. | a•a2=a3 | C. | a6÷a2=a3 | D. | (a2)3=a5 |
1.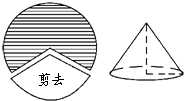 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
 如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )
如图,将半径为15cm的圆形纸片剪去$\frac{2}{5}$圆周的一个扇形,用剩下的扇形围成一个圆锥的侧面(接缝忽略不计),这个圆锥的高是( )| A. | 12cm | B. | 8cm | C. | 20cm | D. | 18cm |
18.若二元一次方程组$\left\{\begin{array}{l}x+y=3\\ 3x-5y=4\end{array}\right.$的解为$\left\{\begin{array}{l}x=a\\ y=b\end{array}\right.$,则a-b=( )
| A. | 1 | B. | 3 | C. | $-\frac{1}{4}$ | D. | $\frac{7}{4}$ |
19.计算6m6÷(-2m2)3的结果为( )
| A. | -m | B. | -1 | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
 某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.
某商场新进一种商品,进货价为30元/件,按物价局规定,商品售价在30~70元之间,(包括30元和70元),经过一段销售发现,商品销量y(件/天)与售价x(元/件)之间满足一次函数关系,如图所示.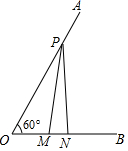 如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )
如图,已知∠AOB=60°,点P在边OA上,OP=10,点M、N在边OB上,PM=PN,若MN=2,则OM=( )