题目内容
9．
已知：如图，E，F在AC上，AD∥CB，AD=CB，AE=CF，求证：∠D=∠B．
分析 由平行线的性质得到，∠A=∠C，由AE=CF，即AF+EF=EF+EC，得到AF=CE，然后根据全等三角形的判定定理SAS证得结论．
解答 证明：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，即AF+EF=EF+EC，
∴AF=CE，
在△AFD和△CEB中，
$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AF=CE}\end{array}\right.$，
∴△AFD≌△CEB，
∴∠D=∠B．
点评 本题考查了平行线的性质，全等三角形的判定与性质，熟记判定定理是解题的关键．
练习册系列答案
相关题目
是同类二次根式的是（ ）
B. 
C. 
D. 
17．我市农业结构调整取得了巨大成功，今年水果又喜获丰收，某果园组织30辆汽车装运A、B、C三种水果共84t到外地销售，规定每辆汽车只装运一种水果，且必须装满；又装运每种水果的汽车不少于4辆；同时，装运的B种水果的汽车辆数不超过装运的A、C两种水果的汽车辆数之和．
（1）设用x辆汽车装运A种水果，用y辆汽车装运B种水果，根据下表提供的信息，求y与x之间的函数关系式并直接写出自变量x的取值范围；
（2）设此次外销活动的利润为Q（百元），求Q与x之间的函数关系式，请你提出一个获得最大利润时的车辆分配方案．
（1）设用x辆汽车装运A种水果，用y辆汽车装运B种水果，根据下表提供的信息，求y与x之间的函数关系式并直接写出自变量x的取值范围；
| 水果品种 | A | B | C |
| 每辆汽车运装量/t | 4 | 3 | 2 |
| 每吨水果获利/百元 | 6 | 8 | 5 |
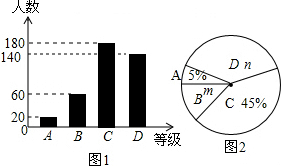
如图，在△ABC中，∠BAC=50°，BD、CE分别是边AC，AB上的高，BD、CE相交于点O，则∠BOC的度数是130°．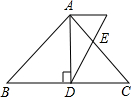
如图，AD是等腰△ABC底边上的高，且AD=4，sinB=$\frac{4}{5}$，若E是AC边上的点，且满足AE：EC=2：3，连接DE，求cot∠ADE的值．
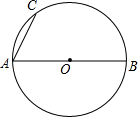如图，AB是⊙O的直径，AC为弦．
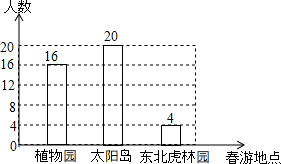某学校准备组织八年级学生春游，供学生选择的春游地点分别是：植物园、太阳岛、东北虎林园．每名学生只能选择其中一个春游地点（必选且只选一个）．该校从八年级学生中随机抽取了a名学生，对他们选择春游地点的情况进行调查，并根据调查结果绘制成如图所示的条形统计图．