题目内容
4. 如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.
如图,在△ABC中,∠BAC=50°,BD、CE分别是边AC,AB上的高,BD、CE相交于点O,则∠BOC的度数是130°.
分析 由垂直的定义得到∠ADB=∠BEC=90°,再根据三角形内角和定理得∠ABD=180°-∠ADB-∠A=180°-90°-60°=30°,然后根据三角形的外角性质有∠BOC=∠EBD+∠BEO,计算即可得到∠BOC的度数.
解答 解:∵BD、CE分别是边AC,AB上的高,
∴∠ADB=∠BEC=90°,
又∵∠BAC=50°,
∴∠ABD=180°-∠ADB-∠A=180°-90°-50°=40°,
∴∠BOC=∠EBD+∠BEO=90°+40°=130°,
故答案为:130°.
点评 本题考查了三角形的外角性质,解决本题的关键是明确三角形的任一外角等于与之不相邻的两内角的和,也考查了垂直的定义以及三角形内角和定理.

练习册系列答案
相关题目
14.下列分式是最简分式的是( )
| A. | $\frac{x-1}{{x}^{2}-x}$ | B. | $\frac{x-1}{x+1}$ | C. | $\frac{x-1}{{x}^{2}-1}$ | D. | $\frac{{a}^{2}bc}{ab}$ |
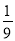 B.
B. 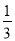 C.
C. 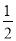 D.
D. 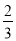
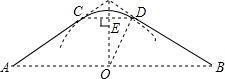 如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米.
如图,某公园的一角有一块草坪(阴影部分),实线部分是沿草坪外围的一条小路,小路由两条相等的线段AC、BD和圆弧CD组成,其中AC、BD分别与圆弧CD相切于点C、D.经过测量,线段CD与半径OD都为60米,则这条小路的长度为120$\sqrt{3}$+2π米. 由几个相同的小正方体组成了一个几何体,该几何体的三视图如图所示,则该几何体可能为( )
由几个相同的小正方体组成了一个几何体,该几何体的三视图如图所示,则该几何体可能为( )



 已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B.
已知:如图,E,F在AC上,AD∥CB,AD=CB,AE=CF,求证:∠D=∠B.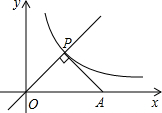 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.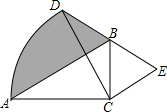 如图,在Rt△ABC中,∠ABC=90°,BC=1,将Rt△ABC绕点C顺时针旋转60°,此时点B恰好在DE上,其中点A经过的路径为弧AD,则图中阴影部分的面积是$\frac{π}{2}$-$\frac{\sqrt{3}}{4}$.
如图,在Rt△ABC中,∠ABC=90°,BC=1,将Rt△ABC绕点C顺时针旋转60°,此时点B恰好在DE上,其中点A经过的路径为弧AD,则图中阴影部分的面积是$\frac{π}{2}$-$\frac{\sqrt{3}}{4}$.