题目内容
在平面直角坐标系xOy中,A点的坐标为(6,3),在OA上有一点B,B点的横坐标为4,M为x轴上任意一点,当MA+MB取最小值时,M点的坐标为 .
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:本题根据题意可知A(6,3)关于x轴的对称点是A′(6,-3),经过A′、B的直线可以求出,这条直线与x轴的交点就是M点.
解答:解:依题意得:A(6,3)关于x轴的对称点是A′(6,-3),
∵A点的坐标为(6,3),
∴直线OA的解析式为y=
x,
∵直线OA经过点B,B点的横坐标为4,
∴y=
×4=2,
∴B(4,2),
设过A′(6,-3)与B(4,2)的直线为:y=kx+b,
∴
解得
,
∴直线AB的解析式为y=-
x+12,
令y=0,得x=
.
故答案为(
,0).
∵A点的坐标为(6,3),
∴直线OA的解析式为y=
| 1 |
| 2 |
∵直线OA经过点B,B点的横坐标为4,
∴y=
| 1 |
| 2 |
∴B(4,2),
设过A′(6,-3)与B(4,2)的直线为:y=kx+b,
∴
|
|
∴直线AB的解析式为y=-
| 5 |
| 2 |
令y=0,得x=
| 24 |
| 5 |
故答案为(
| 24 |
| 5 |
点评:本题主要考查了最短线路问题及坐标与图形的性质;能够正确作出M的位置是解决本题的关键,难度适中.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
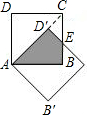 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转,则这两个正方形重叠部分的面积是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用( )次,就可以找到圆形工件的圆心.
如图,MN所在的直线垂直平分线段AB,利用这样的工具,最少使用( )次,就可以找到圆形工件的圆心.| A、1 | B、2 | C、3 | D、4 |
 一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减
一部分同学围在一起做“传数”游戏,我们把某同学传给后面的同学的数称为该同学的“传数”.游戏规则是:同学1心里先想好一个数,将这个数乘以2再加1后传给同学2,同学2把同学1告诉他的数除以2再减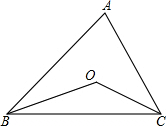 如图,点O是△ABC两内角平分线的交点
如图,点O是△ABC两内角平分线的交点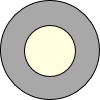 如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化
如图,在一个半径为20厘米的圆面上,从中心挖去一个半径为x厘米的圆面,当挖去的圆的半径由小变大时,剩下的圆环面积也随之变化 如图,在数轴上有若干个点每相邻两点之间的距离是1个单位长,有理数a,b,c,d 所表示的点是其中的4个,且在数轴上的位置如图所示.设3a=4b-3,求c+2d的值.
如图,在数轴上有若干个点每相邻两点之间的距离是1个单位长,有理数a,b,c,d 所表示的点是其中的4个,且在数轴上的位置如图所示.设3a=4b-3,求c+2d的值.