题目内容
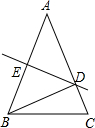 如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到
如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到考点:线段垂直平分线的性质
专题:
分析:先根据中垂线的定义及线段垂直平分线的性质得出AE=BE,AD=BD,进而可得出结论.
解答:解:∵DE是线段AB的中垂线,
∴AE=BE,AD=BD,
∴BD+CD=AD+CD=AC=10cm,
∵△BDC的周长为16cm,
∴BC=16-10=6(cm).
故答案为:AE=BE,AD=BD,线段垂直平分线上任意一点,到线段两端点的距离相等.
∴AE=BE,AD=BD,
∴BD+CD=AD+CD=AC=10cm,
∵△BDC的周长为16cm,
∴BC=16-10=6(cm).
故答案为:AE=BE,AD=BD,线段垂直平分线上任意一点,到线段两端点的距离相等.
点评:本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
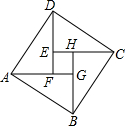 如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )
如图是2002年在北京召开的国际数学家大会的会徽,它由4个相同的直角三角形拼成,已知直角三角形的两条直角边长分别为3和4,则大正方形ABCD和小正方形EFGH的面积比是( )| A、1:5 | B、1:25 |
| C、5:1 | D、25:1 |
关于x的一元二次方程kx2-x+1=0有两个不相等的实数根,则k的取值范围是( )
A、k<
| ||
B、k>
| ||
C、k<
| ||
D、k>
|
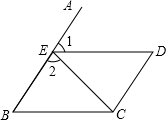 如图,AB∥CD,点E在AB上,且∠1=∠2,∠CED=58°,探究∠BCD为多少度时,DE∥BC?请说明理由.
如图,AB∥CD,点E在AB上,且∠1=∠2,∠CED=58°,探究∠BCD为多少度时,DE∥BC?请说明理由.