题目内容
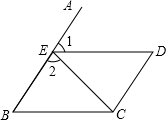 如图,AB∥CD,点E在AB上,且∠1=∠2,∠CED=58°,探究∠BCD为多少度时,DE∥BC?请说明理由.
如图,AB∥CD,点E在AB上,且∠1=∠2,∠CED=58°,探究∠BCD为多少度时,DE∥BC?请说明理由.考点:平行线的判定与性质
专题:
分析:求出∠1和∠2,根据平行线的性质求出∠B,推出∠1=∠B,即可得出答案.
解答:解:当∠BCD=119°时,DE∥BC,
理由是:∵∠1=∠2,∠CED=58°,∠1+∠2+∠CED=180°,
∴∠2=∠1=61°,
∵∠BCD=119°,AB∥CD,
∴∠B=61°,
∴∠1=∠B,
∴DE∥BC.
理由是:∵∠1=∠2,∠CED=58°,∠1+∠2+∠CED=180°,
∴∠2=∠1=61°,
∵∠BCD=119°,AB∥CD,
∴∠B=61°,
∴∠1=∠B,
∴DE∥BC.
点评:本题考查了平行线的性质和判定的应用,注意:平行线的性质是①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
相关题目
计算:(6ab2-4a2b)•3ab的结果是( )
| A、18a2b3-12a3b2 |
| B、18ab3-12a3b2 |
| C、18a2b3-12a2b2 |
| D、18a2b2-12a3b2 |
抛物线y=2(x+3)2-5的顶点坐标是( )
| A、(-3,-5) |
| B、(-3,5) |
| C、(3,-5) |
| D、(3,5) |
在-1
,1.2,-2,0中,负数的个数是( )
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
 如图,直线y=kx+6分别与x轴、y轴相交于点E和点F,点E的坐标为(-8,0),点A的坐标为(0,4).
如图,直线y=kx+6分别与x轴、y轴相交于点E和点F,点E的坐标为(-8,0),点A的坐标为(0,4). 在直角坐标系中直接画出函数y=|x|的图象.若一次函数y=kx+b的图象分别过点A(-1,1)、B(2,2),请你依据这两个函数的图象写出方程组
在直角坐标系中直接画出函数y=|x|的图象.若一次函数y=kx+b的图象分别过点A(-1,1)、B(2,2),请你依据这两个函数的图象写出方程组 如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到
如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到 如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是
如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是