题目内容
已知方程ax2+bx+c=0的两个根为1和-5,则抛物线y=ax2+bx+c的对称轴为直线 .
考点:抛物线与x轴的交点
专题:
分析:根据函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根及两根之和公式来解决此题.
解答:解:∵函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根,
∵x1+x2=-4
则对称轴x=
=-2,
故答案为:x=-2.
∵x1+x2=-4
则对称轴x=
| -4 |
| 2 |
故答案为:x=-2.
点评:本题要求熟悉二次函数与一元二次方程的关系和两根之和公式,并熟练运用.(利用二次函数的对称性解答更直接)

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
抛物线y=2(x+3)2-5的顶点坐标是( )
| A、(-3,-5) |
| B、(-3,5) |
| C、(3,-5) |
| D、(3,5) |
一个QQ群里共有x个好友,每个好友都分别给群里的其他好友发一条信息,共发信息1980条,则可列方程( )
A、
| ||
| B、x(x-1)=1980 | ||
C、
| ||
| D、x(x+1)=1980 |
使分式
的值等于0的x的值是( )
| x2-4 |
| x-2 |
| A、2 | B、-2 | C、±2 | D、±4 |
 已知线段a,b,c.
已知线段a,b,c.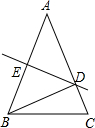 如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到
如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到 如图,AB∥CD,∠A=38°,∠C=80°,求∠M.
如图,AB∥CD,∠A=38°,∠C=80°,求∠M.