题目内容
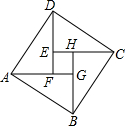如图是2002年在北京召开的国际数学家大会的会徽，它由4个相同的直角三角形拼成，已知直角三角形的两条直角边长分别为3和4，则大正方形ABCD和小正方形EFGH的面积比是（ ）| A、1：5 | B、1：25 |
| C、5：1 | D、25：1 |
考点：勾股定理的证明
专题：
分析：根据勾股定理可得大正方形ABCD的边长，再根据和差关系得到小正方形EFGH的边长，根据正方形的面积公式可得大正方形ABCD和小正方形EFGH的面积，进一步即可求解．
解答：解：如图，设大正方形的边长为xcm，
由勾股定理得32+42=x2，
解得：x=5，
则大正方形ABCD的面积为：52=25；
∵小正方形的边长为：4-3=1，
∴小正方形EFGH的面积为：12=1．
则大正方形ABCD和小正方形EFGH的面积比是25：1．
故选：D．
由勾股定理得32+42=x2，
解得：x=5，
则大正方形ABCD的面积为：52=25；
∵小正方形的边长为：4-3=1，
∴小正方形EFGH的面积为：12=1．
则大正方形ABCD和小正方形EFGH的面积比是25：1．
故选：D．
点评：本题考查勾股定理及正方形的面积公式，比较容易解答，关键是求出大小正方形的边长．
练习册系列答案
阅读快车系列答案
相关题目
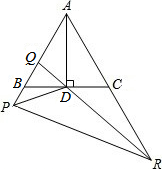如图，在等边△ABC中，AD⊥BC于D，点P在AB的延长线上，点Q在AB上，∠PDQ=60°，QD的延长线交AC的延长线于R（PB＜CR）．若AB=4，PR=7，则PQ=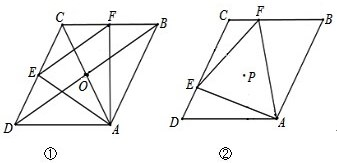
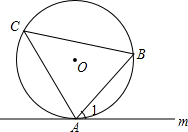如图，直线m与⊙O相切于点A，∠C是弦AB所对的圆周角，试判断∠C与∠1的大小关系．
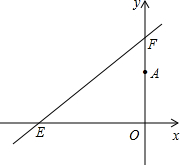如图，直线y=kx+6分别与x轴、y轴相交于点E和点F，点E的坐标为（-8，0），点A的坐标为（0，4）．
已知线段a，b，c．
如图，在△ABC中，∠ABC=∠ACB，P是△ABC内一点，∠BPC=100°，且∠1=∠2．则∠A=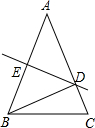
如图，在△ABC中，DE是线段AB的中垂线，由中垂线定义得到