题目内容
当m在什么范围内取值时,二次函数y=x2-2mx+m2-1的图象与x轴的两个交点的横坐标都在-2和4之间?
考点:抛物线与x轴的交点
专题:
分析:根据抛物线的开口方向向上得到,当x=-2、x=4时,y<0,且△>0,据此列出关于m的不等式组,通过解该不等式组可以求得m的取值范围.
解答:解:∵二次函数y=x2-2mx+m2-1的图象开口方向向上,
∴依题意得
,
整理,得
,
故该方程组无解,即这样的m不存在.
∴依题意得
|
整理,得
|
故该方程组无解,即这样的m不存在.
点评:本题考查了抛物线与x轴的交点.根据抛物线的性质列出关于m的不等式组是解题的难点.

练习册系列答案
相关题目
在-1
,1.2,-2,0中,负数的个数是( )
| 1 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
使分式
的值等于0的x的值是( )
| x2-4 |
| x-2 |
| A、2 | B、-2 | C、±2 | D、±4 |
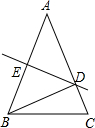 如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到
如图,在△ABC中,DE是线段AB的中垂线,由中垂线定义得到 如图,在一个直径为a+b的半圆中,挖去直径分别为a 和b的两个半圆,则图中阴影部分的面积为
如图,在一个直径为a+b的半圆中,挖去直径分别为a 和b的两个半圆,则图中阴影部分的面积为 如图,四边形ABCD中,∠A=∠C=90°,则经过点A、B、D作⊙O,⊙O是否经过点C?
如图,四边形ABCD中,∠A=∠C=90°,则经过点A、B、D作⊙O,⊙O是否经过点C?