题目内容
6. 如图,AF⊥AB,BC⊥AB,垂足分别为点A,B,点D是AB延长线上一点,且满足AD=BC,DF=CD.
如图,AF⊥AB,BC⊥AB,垂足分别为点A,B,点D是AB延长线上一点,且满足AD=BC,DF=CD.(1)试判断AF与BD的数量关系,并说明理由;
(2)已知点E是BC延长线上一点,且CE=BD,连接AE,若CD=2,求AE的长.
分析 (1)结论:AF=BD.只要证明△DBC≌△FAD即可.
(2)先证明△CDF是等腰直角三角形,求出CF,再证明四边形CEAF是平行四边形即可解决问题.
解答 解:(1)结论:AF=BD.
理由:∵AF⊥AB,BC⊥AB,
∴∠DBC=∠DAF=90°,
在Rt△DBC和Rt△FAD中,
$\left\{\begin{array}{l}{BC=AD}\\{CD=DF}\end{array}\right.$,
∴△DBC≌△FAD,
∴AF=BD.
(2)∵△DBC≌△FAD,
∴∴∠DCB=∠ADF,
∵∠DCB+∠CDB=90°,
∴∠CDB+∠ADF=90°,
∴∠CDF=90°,∵CD=DF=2,
∴CF=$\sqrt{C{D}^{2}+D{F}^{2}}$=2$\sqrt{2}$,
∵EC=DB=AF,EC∥AF,
∴四边形ECFA是平行四边形,
∴AE=CF=2$\sqrt{2}$.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质,勾股定理等知识,解题的关键是正确寻找全等三角形,证明∠CDF是直角是解第二个问题的关键,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 根据下面的三视图,画出这个几何体的平面展开图.
根据下面的三视图,画出这个几何体的平面展开图.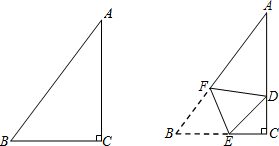
 如图所示,在△ABC中,D是BC上的一点,连接AD,若AC2=CD•BC,则图中有1对相似三角形,分别是△ADC∽△BAC.
如图所示,在△ABC中,D是BC上的一点,连接AD,若AC2=CD•BC,则图中有1对相似三角形,分别是△ADC∽△BAC.