题目内容
10.如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点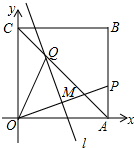
(Ⅰ)若点P的坐标为(1,$\frac{1}{4}$),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由.
分析 (Ⅰ)过M作ME⊥x轴于点E,由三角形中位线定理可求得ME和OE,可求得M点坐标;
(Ⅱ)①同(Ⅰ)容易求得M坐标;②由条件可分别求得直线l和AC的方程,利用图象的交点,可求得Q坐标;
(Ⅲ)可分别用t表示出OQ和OP的长,可证明△OPQ为直角三角形,且OQ=OP,可得到∠QOP=45°.
解答 解:
(Ⅰ)过M作ME⊥x轴于点E,如图1,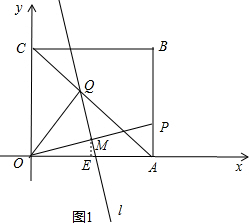
由题意可知M为OP中点,
∴E为OA中点,
∴OE=$\frac{1}{2}$OA=$\frac{1}{2}$,ME=$\frac{1}{2}$AP=$\frac{1}{8}$,
∴M点坐标为($\frac{1}{2}$,$\frac{1}{8}$);
(Ⅱ)①同(Ⅰ),当P(1,t)时,可得M($\frac{1}{2}$,$\frac{1}{2}$t);
②过Q点作QD⊥OA于D,作QE⊥AB与E,连接QP.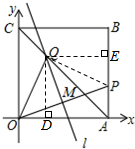
∵Q点在AC上,
∴QD=AD=AE=QE,
在Rt△OQD和Rt△OPE中,
$\left\{\begin{array}{l}{QO=QP}\\{QD=QE}\end{array}\right.$
∴Rt△OQD≌Rt△OPE,
∴OD=PE,
设OD=PE=x,则AD=1-x,AE=t+x,则1-x=t+x,解得x=$\frac{1-t}{2}$,
QD=AE=t+x=$\frac{1+t}{2}$.
∴Q点坐标为($\frac{1-t}{2}$,$\frac{1+t}{2}$).
(Ⅲ)不变化,∠QOP=45°.
理由如下:由(Ⅱ)②可知Q点坐标为($\frac{1-t}{2}$,$\frac{1+t}{2}$),
根据勾股定理得,
OQ2=OD2+QD2=($\frac{1-t}{2}$)2+($\frac{1+t}{2}$)2=$\frac{1+{t}^{2}}{2}$,
QP=OQ,
OP2=OA2+AP2=1+t2,
∴OQ2+QP2=OP2,
∴△OPQ是以OP为斜边的等腰直角三角形,
∴∠QOP=45°,
即∠QOP不变化.
点评 本题主要考查一次函数的综合应用,涉及正方形的性质、待定系数法求函数解析式、三角形中位线定理、直角三角形的判定等知识点.在(Ⅰ)中利用M为OP的中点是解题的关键,在(Ⅱ)②能找出全等是解题关键,在(Ⅲ)中,注意利用(Ⅱ)的结论,求得OQ和OP的长是解题的关键.本题涉及知识点较多,计算量大,有一定的难度.

 如图,根据三视图,判断组成这个物体的块数是( )
如图,根据三视图,判断组成这个物体的块数是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
| A. | 有两个相等的实数根 | B. | 没有实数根 | ||
| C. | 无法确定是否有实数根 | D. | 有两个不相等的实数根 |
| A. | x=0 | B. | x=0或x=5 | C. | x=6 | D. | x=0或x=6 |
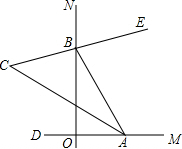 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.