题目内容
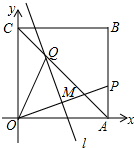
20. 如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
如图,∠MON=90°,点A,B分别在射线OM、ON上移动,BE是∠ABN的平分线,BE的反向延长线与∠OAB平分线相交于点C,试问:∠ACB的大小是否发生变化?如果保持不变,请给出证明;如果随点A、B移动发生变化,请求出变化范围.
分析 根据角平分线的定义、三角形的内角和、外角性质求解.
解答 解:∠ACB的大小保持不变.理由:
∵∠ABn=90°+∠OAB,AC平分∠OAB,BE平分∠ABN,
∴∠ABE=$\frac{1}{2}$∠ABN=$\frac{1}{2}$(90°+∠OAB)=45°+$\frac{1}{2}$∠OAB,
即∠ABE=45°+∠CAB,
又∵∠ABE=∠ACB+∠CAB,
∴∠ACB=45°,
故∠ACB的大小不发生变化,且始终保持45°.
点评 本题考查的是三角形内角与外角的关系,解答此题目要注意:
①求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件;
②三角形的外角通常情况下是转化为内角来解决.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
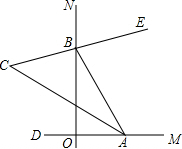
10.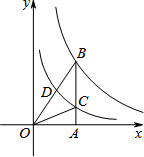 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )| A. | ($\frac{3}{2}$,$\frac{5}{9}$) | B. | ($\frac{\sqrt{5}}{3}$,$\frac{\sqrt{5}}{2}$) | C. | ($\frac{4}{3}$,$\frac{5}{4}$) | D. | ($\frac{\sqrt{10}}{3}$,$\frac{\sqrt{10}}{2}$) |
11.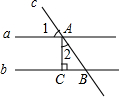 如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
 如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
9.若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
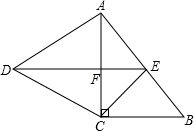 如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.
如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.
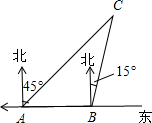 如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里(结果保留根号).
如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是20$\sqrt{2}$海里(结果保留根号).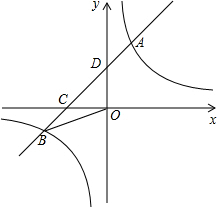 如图,在平面直角坐标系中,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点,与x轴交于点C,与y轴交于点D,已知点B的坐标为(-5,-2),C为BD的中点.
如图,在平面直角坐标系中,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点,与x轴交于点C,与y轴交于点D,已知点B的坐标为(-5,-2),C为BD的中点.