题目内容
1.△ABC和△BCD都是直角三角形,其中∠ACB=∠D=90°,AC=3,BC=4.若两个直角三角形相似,则BD的长为$\frac{12}{5}$或$\frac{16}{5}$.分析 先利用勾股定理计算出AB=5,再分类讨论:当△ABC∽△BCD时,则$\frac{AC}{BD}$=$\frac{AB}{BC}$;当△ABC∽△CBD时,则$\frac{BC}{BD}$=$\frac{AB}{BC}$,然后利用比例性质分别计算出BD的长.
解答 解:∵∠ACB=90°,AC=3,BC=4.
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5,
当△ABC∽△BCD时,$\frac{AC}{BD}$=$\frac{AB}{BC}$,即$\frac{3}{BD}$=$\frac{5}{4}$,解得BD=$\frac{12}{5}$;
当△ABC∽△CBD时,$\frac{BC}{BD}$=$\frac{AB}{BC}$,即$\frac{4}{BD}$=$\frac{5}{4}$,解得BD=$\frac{16}{5}$,
即BD的长为$\frac{12}{5}$或$\frac{16}{5}$.
故答案为$\frac{12}{5}$或$\frac{16}{5}$.
点评 本题考查了相似三角形的性质:相似三角形的对应角相等,对应边的比相等;相似三角形(多边形)的周长的比等于相似比;相似三角形的对应线段(对应中线、对应角平分线、对应边上的高)的比也等于相似比;相似三角形的面积的比等于相似比的平方.注意分类讨论思想的运用.

练习册系列答案
相关题目
11.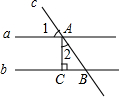 如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
 如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )
如图,直线c与直线a、b交于点A、B,且a∥b,线段AC垂直于直线b,垂足为点C.若∠1=55°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
9.若△ABC∽△DEF,相似比为1:2,且△ABC的面积为2,则△DEF的面积为( )
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
16.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
| A. | a,$\frac{{a}_{3}}{2}$ | B. | a,$\frac{{a}_{3}+{a}_{4}}{2}$ | C. | $\frac{5}{6}$a,$\frac{{a}_{3}+{a}_{4}}{2}$ | D. | $\frac{5}{6}$a,$\frac{{a}_{3}}{2}$ |
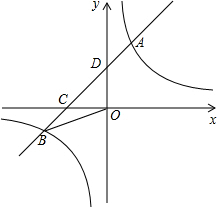 如图,在平面直角坐标系中,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点,与x轴交于点C,与y轴交于点D,已知点B的坐标为(-5,-2),C为BD的中点.
如图,在平面直角坐标系中,一次函数y=ax+b与反比例函数y=$\frac{k}{x}$的图象交于一、三象限的A、B两点,与x轴交于点C,与y轴交于点D,已知点B的坐标为(-5,-2),C为BD的中点.