题目内容
4.三角形的两边长为10和12,那么它的第三边长x的取值范围是2<x<10.分析 根据三角形三边关系:任意两边之和大于第三边以及任意两边之差小于第三边,即可得出第三边的取值范围.
解答 解:∵此三角形的两边长分别为3和6,
∴第三边长的取值范围是:12-10<x<12+10,
即:2<x<10.
故答案为:2<x<10.
点评 此题主要考查了三角形三边关系,根据第三边的范围是:大于已知的两边的差,而小于两边的和是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.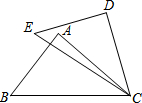 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
 已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )
已知:如图,在△ABC与△DEC中,∠A=∠D,还需要添加两个条件才能使得△ABC≌△DEC,则错误的是( )| A. | AB=DE,∠B=∠E | B. | AB=DE,AC=DC | C. | BC=EC,∠BCE=∠ACD | D. | BC=EC,AC=DC |
9.下列函数(1)y=x;(2)y=2x-1;(3)y=$\frac{1}{x}$;(4)x+y=1中,是一次函数的有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
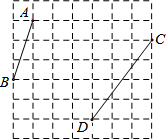 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.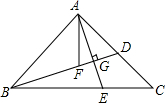 如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由.
如图,在△ABC中,AB=AC,∠BAC=90°,点D是AC边上的一点,连结BD,作AE⊥BD交BC于点E,交BD于点G,AF平分∠BAC交BD于点F,试说明AE=BF的理由. 如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC.
如图,AB∥CD,DF交AC于点E,交AB于点F,DE=EF.求证:AE=EC.