题目内容
14.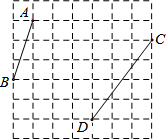 如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中,有线段AB和线段CD,点A、B、C、D均在小正方形的顶点上.(1)在方格纸中画出以AB为一边的等腰直角△ABE,点E在小正方形的顶点上,且∠B为直角;
(2)在方格纸中画出以CD为腰的等腰△CDF,点F在小正方形的顶点上,且△CDF的面积为10.连接EF,请直接写出线段EF的长.
分析 (1)由勾股定理得出$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,由勾股定理的定理得出∠B=90°,画出图形即可;
(2)由勾股定理得出CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,由$\frac{1}{2}$×5×4=10,CF=5,得出△CDF即为所求;由勾股定理求出EF即可.
解答 解:(1)AB=BE=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,AB2+BE2=20=AE2,
∴∠B=90°,如图所示:△ABE即为所求;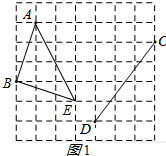
(2)∵CD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
$\frac{1}{2}$×5×4=10,CF=5,
△CDF即为所求,
如图2所示;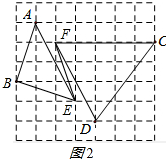
由勾股定理得:EF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$.
点评 本题考查了勾股定理、勾股定理的逆定理、等腰直角三角形的性质、等腰三角形的性质;熟练掌握勾股定理,并能进行计算与作图是解决问题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
8.若将分式$\frac{2x}{x-y}$的分子、分母中的字母的系数都扩大10倍,则分式的值( )
| A. | 扩大10倍 | B. | 扩大10倍 | C. | 不变 | D. | 缩小10倍 |
10.下列图形中,可以作为正方体展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,在△ABC中,AI和CI分别平分∠BAC和∠BCA,如果∠B=58°,那么∠AIC=119°.
如图,在△ABC中,AI和CI分别平分∠BAC和∠BCA,如果∠B=58°,那么∠AIC=119°.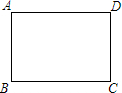 如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5.
如图,已知矩形ABCD中,AB=3,AD=4.以点A为圆心画⊙A,要使点B、C、D中只有两点在⊙A内,那么⊙A半径r的取值范围是3<r<5.