��Ŀ����
11��ij��˾������Ӫָ��y����������˾���Ĺ���ҵ������Ӫָ����y�������������n����ƽ���ٶȣ�x��֮�������ϵʽΪy=ax2+bnx+100����n=1��x=30ʱ��y=190����n=2��x=40ʱ��y=420����1���ú�x��n��ʽ�ӱ�ʾy��
��2�������������Ϊ3�Σ����������Ӫָ��ʱ��ƽ���ٶȣ�
��3����n=2��x=40���ܷ���n����m%��m��0����ͬʱx����m%������£���y��ֵ���ֲ��䣿���ܣ����m��ֵ�������ܣ���˵�����ɣ�
�ο���ʽ��������y=ax2+bx+c��a��0���Ķ��������ǣ�-$\frac{b}{2a}$��$\frac{{4ac-{b^2}}}{4a}$��
���� ��1���ѵ�n=1��x=30ʱ��y=190����n=2��x=40ʱ��y=420������y=ax2+bnx+100���ⷽ���鼴�ɵõ����ۣ�
��2����n=3���룬ȷ��������ϵʽ��Ȼ����y���ֵʱx��ֵ���ɣ�
��3�����������г���ϵʽ�������y=420ʱm��ֵ���ɣ�
��� �⣺��1���������ɵã�$\left\{{\begin{array}{l}{190=900a+30b+100}\\{420=1600a+80b+100}\end{array}}\right.$
���$\left\{{\begin{array}{l}{a=-\frac{1}{10}}\\{b=6}\end{array}}\right.$��
��$y=-\frac{1}{10}{x^2}+6nx+100$��
��2����n=3ʱ��$y=-\frac{1}{10}{x^2}+18x+100$��
��$a=-\frac{1}{10}��0$��֪��Ҫʹy���$x=-\frac{18}{{2����-\frac{1}{10}��}}=90$��
��3����n=2��x=40����$y=-\frac{1}{10}{x^2}+6nx+100$���ɵ�y=420��
�������⣬��$420=-\frac{1}{10}{[40��1-m%��]^2}+6��2��1+m%����40��1-m%��+100$��
��2��m%��2-m%=0
���m%=$\frac{1}{2}$����m%=0����ȥ��
��m=50��
���� ���⿼���˶��κ�����Ӧ�ã��ѶȽϴ����Ĺؼ��Ǹ�����Ŀ����������Ϣ�����������г�������ϵʽ��Ҫ��ͬѧ����������κ�����ֵ�ķ�����������鷳������ѧ��������ѧ֪ʶ���ʵ�����������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�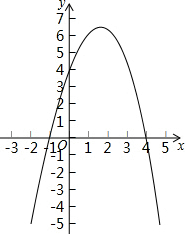 ��֪���κ���y=-x2+3x+4��ͼ����ͼ����ֱ��д�𰸣�
��֪���κ���y=-x2+3x+4��ͼ����ͼ����ֱ��д�𰸣�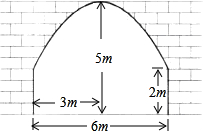 ij������϶�������������ε�������ɣ��ߴ���ͼ��ʾ��
ij������϶�������������ε�������ɣ��ߴ���ͼ��ʾ�� ��ͼ��һλ�����˶�Ա�ھ�����Ȧ����ˮƽ����4m������Ͷ��������һ���������˶��������˶���ˮƽ����Ϊ2.5mʱ���ﵽ���߶�3.5m��Ȼ��ȷ���������ڣ���֪��Ȧ���ľ������߶�Ϊ3.05m���Խ���������⣺
��ͼ��һλ�����˶�Ա�ھ�����Ȧ����ˮƽ����4m������Ͷ��������һ���������˶��������˶���ˮƽ����Ϊ2.5mʱ���ﵽ���߶�3.5m��Ȼ��ȷ���������ڣ���֪��Ȧ���ľ������߶�Ϊ3.05m���Խ���������⣺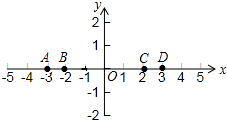 ��ͼ��ʾ��C��D����ĺ�����ֱ�Ϊ2��3���߶�CD=1��B��D����ĺ�����ֱ�Ϊ-2��3���߶�BD=5��A��B����ĺ�����ֱ�Ϊ-3��-2���߶�AB=1����̽����
��ͼ��ʾ��C��D����ĺ�����ֱ�Ϊ2��3���߶�CD=1��B��D����ĺ�����ֱ�Ϊ-2��3���߶�BD=5��A��B����ĺ�����ֱ�Ϊ-3��-2���߶�AB=1����̽����

 ��a��0����ͼ�����������㣬����һ�����������Ϊ��-3��-2��������һ�����������Ϊ�� ��
��a��0����ͼ�����������㣬����һ�����������Ϊ��-3��-2��������һ�����������Ϊ�� ��